题目内容
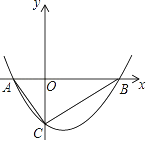
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式;
(2)判断△ABC的形状,证明你的结论.
【答案】(1)y= ![]() x2﹣
x2﹣ ![]() x﹣2;(2)见解析
x﹣2;(2)见解析
【解析】试题分析:(1)因为点A在抛物线上,所以将点A代入函数解析式即可求得;
(2)由函数解析式可以求得其与x轴、y轴的交点坐标,即可求得AB、BC、AC的长,由勾股定理的逆定理可得三角形的形状.
试题解析:(1)∵点A(-1,0)在抛物线y=![]() x2+bx-2上,
x2+bx-2上,
∴![]() ×(-1)2+b×(-1)-2=0,b=-
×(-1)2+b×(-1)-2=0,b=-![]()
∴抛物线的解析式为y=![]() x2-
x2-![]() x-2
x-2
(2)当x=0时y=-2,
∴C(0,-2),OC=2.
当y=0时, ![]() x2-
x2-![]() x-2=0,
x-2=0,
∴x1=-1,x2=4,
∴B(4,0).
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目