题目内容
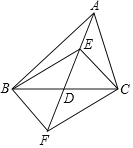
【题目】等腰△ABD中,AD=BD,将△ABD绕腰BD的中点顺时针旋转180°,得到△CDB,CE平分∠BCD交BD于点E,在BC的延长线上取点F,使CF=DE,连接EF交CD于点G.
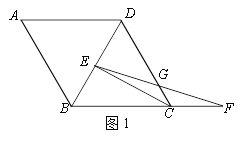
(1)如图1,∠A=60°,AB=4,求CF的长;
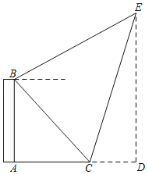
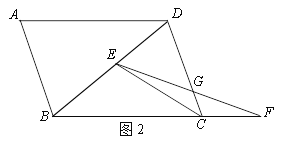
(2)如图2,求证:DE=2CG.
【答案】(1)CF=2;(2)详见解析
【解析】
(1)先证明△ABD是等边三角形,再根据旋转的性质得到△CBD是等边三角形,根据等腰三角形的三线合一的性质即可得到CF的长;
(2)过点E作EM∥BC,交CD于点M,利用平行线的性质及等腰三角形的性质得到DE=EM=CF,由此证明△EMG≌△FCG,再利用角平分线的性质即可得到结论.
(1)解:∵AD=BD,∠A=60°
∴△ABD是等边三角形
∴∠ADB=60°,BD =4
由旋转性质知,得△ABD≌△CDB
∴△CBD是等边三角形
且CE平分∠BCD
∴BE=DE=2
∵CF=DE
∴CF=2
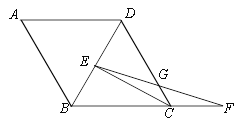
(2)过点E作EM∥BC,交CD于点M,
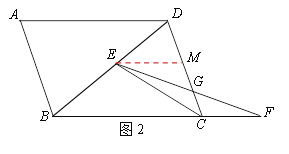
∴∠DME=∠DCB, ∠MEG=∠F, ∠ECB=∠MEC,
∵BD=CB,
∴∠BDC=∠BCD=∠DME,
∴DE=EM=CF,
在△EMG和△FCG中
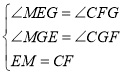 ,
,
∴△EMG≌△FCG,
∴MG=CG,
∵CE平分∠BCD,
∴∠ECB=∠ECM=∠MEC,
∴EM=MC=2CG,
∴DE=2GC.

练习册系列答案
相关题目