题目内容
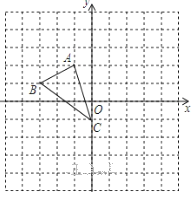
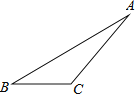
【题目】如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕A顺时针旋转60°得
绕A顺时针旋转60°得![]() .
.
(1)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)求BE的长度.
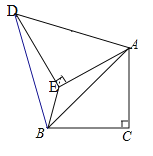
【答案】(1)等边三角形;(2)![]()
【解析】
(1)根据旋转的性质得AB=AD,∠BAD=60°,则可判断△![]() 是等边三角形;
是等边三角形;
(2)延长BE交AB′AD于F,如图,在Rt△ADE中,利用等腰直角三角形斜边上的中线性质得EF=![]() AB=1,再根据等边三角形的性质得BD=
AB=1,再根据等边三角形的性质得BD=![]() AD=
AD=![]() ,然后计算BF-EF即可.
,然后计算BF-EF即可.
解:(1)△![]() 是等边三角形.理由如下:
是等边三角形.理由如下:
∵![]() 绕A顺时针旋转60°得
绕A顺时针旋转60°得![]() ,
,
∴AB=AD,∠BAD=60°,
∴△ABB′是等边三角形;
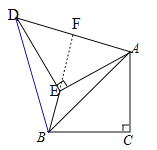
(2)延长BE交AD于F,如图,
![]() 绕A顺时针旋转60°得
绕A顺时针旋转60°得![]() ,
,
∴AE=DE=![]()
由(1)有AB=BD,
而DE=BC,
∴BE垂直平分AD;
在Rt△ADE中,AD=![]() AE=2,
AE=2,
∴EF=![]() AB=1,
AB=1,
∵BF为等边![]() 的高,
的高,
∴BF=![]() AD=
AD=![]() ,
,
∴BE=BF-EF=![]() .
.

练习册系列答案
相关题目