题目内容
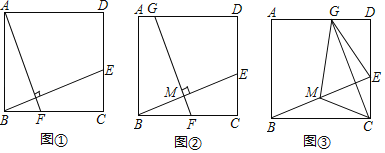
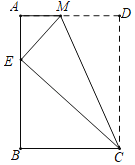
【题目】如图,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若△AEM与△ECM相似,则AB和BC的数量关系为_____.
【答案】BC![]() AB.
AB.
【解析】
分两种情况,当∠AEM=∠EMC时,△AEM∽△ECM,则AE∥MC,不合题意舍去;当∠AEM=∠MCE时,△AEM∽△ECM,针对这种情况将AM,MD分别用含CD的代数式表示出来,然后通过矩形建立AB和BC的关系.
∵矩形ABCD沿CM折叠,使点D落在AB边上的点E处,
∴∠MEC=∠D=90°,∠DMC=∠EMC,ME=MD,
∴∠A=∠MEC,
当∠AEM=∠EMC时,△AEM∽△ECM,则AE∥MC,不合题意舍去;
当∠AEM=∠MCE时,△AEM∽△ECM,∠AME=∠EMC,此时∠DMC=∠EMC=∠AME=60°,
在Rt△CDM中,MD![]() CD,
CD,
∴EM![]() CD,
CD,
在Rt△AEM中,AM![]() EM
EM![]() CD,
CD,
∴AD=AM+DM![]() CD
CD![]() CD
CD![]() CD,
CD,
∵四边形ABCD为矩形,
∴AB=CD,BC=AD,
∴BC![]() AB.
AB.
故答案为BC![]() AB.
AB.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目