Question

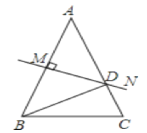
【题目】已知：如图，AB=AC，∠A=36°，AB的垂直平分线交AC于D，则下列结论：①∠C=72°；②BD是∠ABC的平分线；③△ABD是等腰三角形；④△BCD是等腰三角形，其中正确的有____

Answer 1

【答案】①②③④

【解析】

根据等腰三角形性质易得∠ABC=∠C=72°；根据线段垂直平分线性质知，AD=DB，∠ABD=∠A=36°，判定②③正确；根据三角形内角和定理得∠BDC=72°=∠C，所以BD=BC，判定④正确．

∵AB=AC，∠A=36°，

∴∠ABC=∠C=72°.故①正确；

∵MN垂直平分AB，∴DB=DA，即△ABD是等腰三角形，故③正确；

∴∠ABD=∠A=36°，

∴∠CBD=72°36°=36°=∠ABD，故②正确；

∵∠BDC=180°36°72°=72°=∠C，

∴BC=BD，即△BCD是等腰三角形，故④正确.

故答案为①②③④