��Ŀ����
����Ŀ����֪����ͼ����ֱ֪�� AB �ĺ�������ʽΪ y 2x 8 ���� x �ύ�ڵ� A ���� y�ύ�ڵ� B ��
��1���� A �� B ��������ꣻ
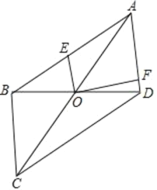
��2������ P m, nΪ�߶� AB �ϵ�һ�����㣨�� A ��B ���غϣ����� PE x ���� E �� PF y���ڵ� F ������ EF ���ʣ�
����PEF �����Ϊ S ���� S ���� m �ĺ�����ϵʽ��������� S 3ʱ P ������ꣻ
���Ƿ���ڵ� P ��ʹ EF ��ֵ��С�������ڣ���� EF ����Сֵ���������ڣ���˵�����ɡ�

���𰸡���1��A��4��0����B��0��8������2����![]() �������ڣ�EF����Сֵ=OP=
�������ڣ�EF����Сֵ=OP=![]() .
.
��������
��1�������������ϵ���ص�ֱ����ֵ��
��2�����ɵ���ֱ��AB�ϣ��ҳ�m��n�Ĺ�ϵ�����������ε������ʽ��⼴�ɣ�
�ڴ��ڣ�����֤���ı���OEPF�Ǿ��Σ��ɵ�EF=OP�����ݴ��߶���̿�֪����OP��ABʱ����ʱEF��С��
�⣺��1����x=0����y=8��
��B��0��8����
��y=0����-2x+8=0��
��x=4��
��A��4��0����
��2���١ߵ�P��m��n��Ϊ�߶�AB�ϵ�һ�����㣬
��-2m+8=n��
��A��4��0����
��OA=4��
��0��m��4
��PF=m��PE=-2m+8
��![]() =
=![]() PF��PE=
PF��PE=![]() ��m����-2m+8��=
��m����-2m+8��=![]() ����0��m��4����
����0��m��4����
�ڴ��ڣ���ͼ
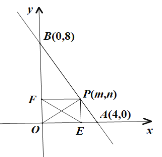
���ɣ���PE��x���ڵ�E��PF��y���ڵ�F��OA��OB��
���ı���OEPF�Ǿ��Σ�
��EF=OP��
��OP��ABʱ����ʱEF��С��
��A��4��0����B��0��8����
��AB=![]()
��S��AOB=![]() ��OA��OB=
��OA��OB=![]() ��AB��OP��
��AB��OP��
![]() ��
��
��EF����Сֵ=OP=![]() .
.