题目内容
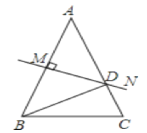
【题目】如图,一伞状图形,已知∠AOB=120°,点P是∠AOB角平分线上一点,且OP=2,∠MPN=60°,PM与OB交于点F,PN与OA交于点E.
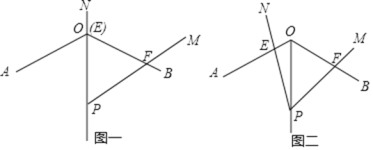
(1)如图一,当PN与PO重合时,探索PE,PF的数量关系.
(2)如图二,将∠MPN在(1)的情形下绕点P逆时针旋转a度(0<a<60°),继续探索PE,PF的数量关系,并求四边形OEPF的面积.
【答案】(1)PE=PF;(2)![]() .
.
【解析】
(1)根据角平分线定义得到∠POF=60°,推出△PEF是等边三角形,得到PE=PF;
(2)过点P作PQ⊥OA,PH⊥OB,根据角平分线的性质得到PQ=PH,∠PQO=∠PHO=90°,根据全等三角形的性质得到PE=PF,S四边形OEPF=S四边形OQPH,求得OQ=1,QP=![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
解:(1)∵∠AOB=120°,OP平分∠AOB,
∴∠POF=60°,
∵∠MPN=60°,∴MPN=∠FOP=60°,∴△PEF是等边三角形,
∴PE=PF;
(2)过点P作PQ⊥OA,PH⊥OB,
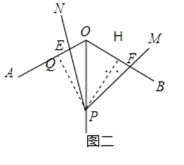
∵OP平分∠AOB,
∴PQ=PH,∠PQO=∠PHO=90°,
∵∠AOB=120°,∴∠QPH=60°,
∴∠QPE+∠FPH+∠EPH, ∴∠QPE=∠EPF,
在△QPE与△HPF中
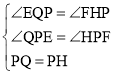 ,
,
∴△QPE≌△HPF(AAS),
∴PE=PF,
S四边形OEPF=S四边形OQPH,
∵PQ⊥OA,PH⊥OB,OP平分∠AOB,∴∠QPO=30°,
∴OQ=1,QP=![]() =
=![]() ,∴S△OPQ=
,∴S△OPQ=![]() ×1×
×1×![]() =
=![]() ,
,
∴四边形OEPF的面积=2S△OPQ=![]()

练习册系列答案
相关题目