题目内容
【题目】某校八年级数学实践能力考试选择项目中，选择数据收集项目和数据分析项目的学生比较多。为了解学生数据收集和数据分析的水平情况，进行了抽样调查，过程如下，请补充完整.收集数据：从选择数据收集和数据分析的学生中各随机抽取16人，进行了体育测试，测试成绩（十分制）如下：
数据收集 | 10 | 9.5 | 9.5 | 10 | 8 | 9 | 9.5 | 9 | 7 | 10 | 4 | 5.5 | 10 | 7.9 | 9.5 | 10 |
数据分析 | 9.5 | 9 | 8.5 | 8.5 | 10 | 9.5 | 10 | 8 | 6 | 9.5 | 10 | 9.5 | 9 | 8.5 | 9.5 | 6 |
整理，描述数据：按如下分数段整理，描述这两组样本数据：
|
|
|
| 10 | |
数据收集 | 1 | 1 | 3 | 6 | 5 |
数据分析 |
（说明：成绩8.5分及以上为优秀，6分及以上为合格，6分以下为不合格.）
分析数据：两组样本数据的平均数，中位数，众数如下表所示：
项目 | 平均数 | 中位数 | 众数 |
数据收集 | 8.75 | 9.5 | 10 |
数据分析 | 8.81 | 9.25 | 9.5 |
得出结论：
（1）如果全校有480人选择数据收集项目，达到优秀的人数约为________人；
（2）初二年级的井航和凯舟看到上面数据后，井航说：数据分析项目整体水平较高.凯舟说：数据收集项目整体水平较高.你同意________的看法，理由为_______________________.（至少从两个不同的角度说明推断的合理性）
【答案】（1）330；（2）凯舟，数据收集项目的中位数较大，众数也较大，因此数据收集项目的整体水平较高．
【解析】
（1）样本估计总体，样本中优秀人数占调查人数的
，估计480人的得优秀；
（2）可从中位数、众数的角度进行分析得出答案．
解：整理的表格如下：
（1）480×
=330人，
故答案为：330．
（2）根据以下表格可知：
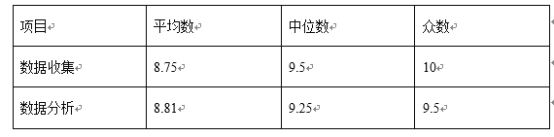
根据整理后的数据，我同意凯舟的说法，数据收集项目的中位数较大，众数也较大，因此数据收集项目的整体水平较高．
故答案为：凯舟；数据收集项目的中位数较大，众数也较大，因此数据收集项目的整体水平较高．
