题目内容
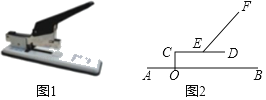
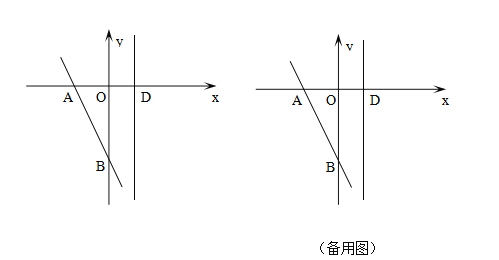
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图像经过点A(-2,0),B(0,-2![]() )、过D(1,0)作平行于y轴的直线l;
)、过D(1,0)作平行于y轴的直线l;
(1) 求一次函数y=kx+b的表达式;
(2)若P为y轴上的一个动点,连接PD,则![]() 的最小值为____ ____.
的最小值为____ ____.
(3)M(s,t)为直线l上的一个动点,若平面内存在点N,使得A、B、M、N为顶点的四边形为矩形,则求M,N点的坐标;
【答案】(1)![]() ;(2)
;(2)![]() ;(3)M(1,
;(3)M(1,![]() ),N(-3,
),N(-3,![]() )或M(1,
)或M(1,![]() ),N(-3,
),N(-3,![]() );或M(1,
);或M(1,![]() ),N(-3,
),N(-3,![]() ).
).
【解析】
(1)把A(-2,0),B(0,-2![]() )代入y=kx+b中解出即可;
)代入y=kx+b中解出即可;
(2)过点D作DE⊥AB于点E,交y轴于点P,此时![]() 值最小,求出DE长即可;
值最小,求出DE长即可;
(3)得到M坐标为(1,t),则![]() ,
,![]() ,
,![]() ,得A、B、M、N为顶点的四边形为矩形,则分类讨论:①∠AMB=90°,即
,得A、B、M、N为顶点的四边形为矩形,则分类讨论:①∠AMB=90°,即![]() ;②∠MAB=90°,即
;②∠MAB=90°,即![]() ;③∠MBA=90°,即
;③∠MBA=90°,即![]() 分别求出t即可求出M,N的坐标.
分别求出t即可求出M,N的坐标.
(1)把A(-2,0),B(0,-2![]() )代入y=kx+b,
)代入y=kx+b,
可得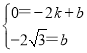 ,解得
,解得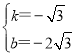 ,
,
∴直线AB的函数表达式为![]() ;
;
(2)过点D作DE⊥AB于点E,交y轴于点P,
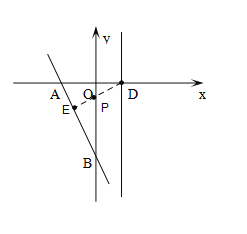
此时![]() 值最小,
值最小,
∵A(-2,0),B(0,-2![]() ),
),
∴OA=2,OB=2![]() ,
,
∴tan∠ABO=![]() ,
,
∴∠ABO=30°,
∵DE⊥AB,
∴PE=![]() ,
,
![]() ,
,
∴DE⊥AB于点E,交y轴于点P时,![]() 取最小值,
取最小值,
∵∠AOB=90°,
∴∠DAE=60°,
∵AD=3,
∴![]() ,
,
∴![]() 的最小值为:
的最小值为:![]() ;
;
(3)∵M(s,t)为直线l上的一个动点,
∴M坐标为(1,t),
∴![]() ,
,
∴![]() ,
,![]() ,
,
使得A、B、M、N为顶点的四边形为矩形,则分类讨论:
①∠AMB=90°,即![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴M(1,![]() ),
),
则M(1,![]() )到B(0,-2
)到B(0,-2![]() )是向左一个单位,向下
)是向左一个单位,向下![]() 个单位,
个单位,
∵A(-2,0),
∴N(-3,![]() );
);
②∠MAB=90°,即![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴M(1,![]() ),
),
则M(1,![]() )到B(0,-2
)到B(0,-2![]() )是向左一个单位,向下
)是向左一个单位,向下![]() 个单位,
个单位,
∵A(-2,0),
∴N(-3,![]() );
);
③∠MBA=90°,即![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴M(1,![]() ),
),
则M(1,![]() )到B(0,-2
)到B(0,-2![]() )是向左一个单位,向下
)是向左一个单位,向下![]() 个单位,
个单位,
∵A(-2,0),
∴N(-3,![]() );
);
综上,M(1,![]() ),N(-3,
),N(-3,![]() )或M(1,
)或M(1,![]() ),N(-3,
),N(-3,![]() );或M(1,
);或M(1,![]() ),N(-3,
),N(-3,![]() ).
).

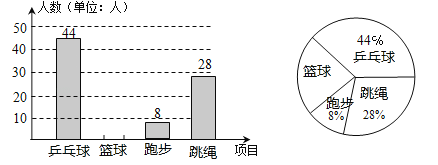
【题目】某单位需招聘一名技术员,对甲、乙、丙三名候选人进行了笔试和面试两项测试,其成绩如下表所示.根据录用程序,该单位又组织了![]() 名人员对三人进行民主评议,其得票率如扇形图所示,每票
名人员对三人进行民主评议,其得票率如扇形图所示,每票![]() 分(没有弃权票。每人只能投
分(没有弃权票。每人只能投![]() 票)
票)
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
笔试 |
|
|
|
面试 |
|
|
|
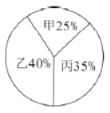
(1)请算出三人的民主评议得分.
(2)该单位将笔试、面试、民主评议三项得分按![]() 确定综合成绩,且民主评议得分低于
确定综合成绩,且民主评议得分低于![]() 分不录取,谁将被录用?请说明理由.
分不录取,谁将被录用?请说明理由.