题目内容
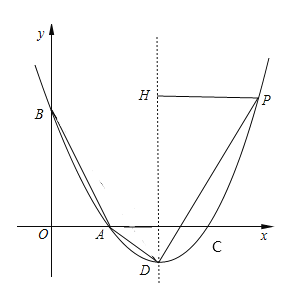
【题目】如图，已知抛物线
经过点A（1，0）和B（0，3），其顶点为D．设P为该抛物线上一点，且位于抛物线对称轴右侧，作PH⊥对称轴，垂足为H，若△DPH与△AOB相似
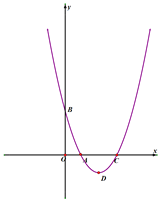
（1）求抛物线的解析式
（2）求点P的坐标
【答案】（1）y=x2-4x+3；（2）（5，8）或（
，-
）．
【解析】
（1）利用待定系数法求抛物线解析式；
（2）设P（x，x2-4x+3）（x＞2），则H（2，x2-4x+3），分别表示出PH和HD，分
时，
时两种情况分别求出x即可.
解：（1）把A（1，0）和B（0，3）代入y=x2+bx+c得
，解得
，
∴抛物线解析式为y=x2-4x+3；
（2）抛物线的对称轴为直线x=2，
设P（x，x2-4x+3）（x＞2），则H（2，x2-4x+3），
∴PH=x-2，HD=x2-4x+3-（-1）=x2-4x+4，
∵∠PHD=∠AOB=90°，
∴当 时，△PHD∽△AOB，即
，
解得x1=2（舍去），x2=5，此时P点坐标为（5，8）；
当 时，△PHD∽△BOA，即
，
解得x1=2（舍去），x2= ，此时P点坐标为（，-）；
综上所述，满足条件的P点坐标为（5，8）或（，-）．
练习册系列答案
相关题目
