题目内容
【题目】综合与实践:“四扇纸风车”的制作
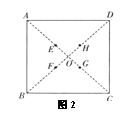
阅读“四扇纸风车”的制作过程,解决下列问题:“四扇纸风车”是如何制作的呢?如图1,首先,裁剪一块边长为12cm的正方形纸张;将花纹面朝下,使用你的尺子,画两条对角线(或沿其对角线对折);找到对角线的交点O,用按钉按下做个标记;在被交点O所分成的四条线段上靠近交点O的三等分点处分别做标记;如图2,然后由正方形的每个角开始延对角线剪开,到记号处停下;这样就有8个可折叠的角,将不相邻的四个角(不相邻指两角中间隔一角)折向中心;再用铁丝或钉子把它固定在一根木棍上就制作好了。

任务一:
(1)如图2 是制作过程中在对角线上做好标记的示意图,请求出正方形每个角处沿对角线剪开的长度;
(2)求出标记点E到正方形ABCD的顶点B的距离。
任务二:
若将“距交点O的![]() 处做标记”改为“距交点O的
处做标记”改为“距交点O的![]() 处做标记”并将不相邻的四个角折叠、压平,使角的顶点与交点O 重合,其余条件不变。
处做标记”并将不相邻的四个角折叠、压平,使角的顶点与交点O 重合,其余条件不变。
(1)请在图3中,把“四扇纸风车”的示意图补充完整,并将重叠部分图上阴影;
(2)求出(1)中补充完整后的“四扇纸风车”示意图中重叠部分的面积。
【答案】任务一:(1)![]() cm;(2)
cm;(2)![]() cm;任务二:(1)补图见解析;(2)
cm;任务二:(1)补图见解析;(2)![]()
【解析】
试题分析:任务一:(1)解直角三角形即可求解;(2)运用勾股定理求解即可;任务二:(1)补图即可;(2)由题意可知:重叠部分三角形是等腰直角三角形,且四个三角形的面积相等。求出一个,即可求出全面积.
试题解析:任务一:
(1)∵四边形ABCD是正方形,
∴![]()
在![]() 中,
中,![]() ∴
∴![]()
∴![]()
∴正方形每个角处沿对角线剪开的长度为![]() cm
cm
(2)连接BE,
∵四边形ABCD是正方形,![]()
∴![]()
∴![]()
∴标记点E到正方形ABCD的顶点B的距离为![]() cm。
cm。
任务二:
(1)如图所示:
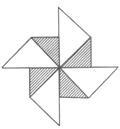
(2)由题意可知:重叠部分三角形是等腰直角三角形,且四个三角形的面积相等。
其中一块重叠部分的面积为:![]()
∴“四扇纸风车”示意图中重叠部分的面积为:![]()

 金钥匙试卷系列答案
金钥匙试卷系列答案