题目内容
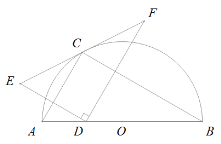
【题目】 如图点![]() 在以
在以![]() 为直径的半圆的圆周上,若
为直径的半圆的圆周上,若![]()
![]() 为边
为边![]() 上一动点,点
上一动点,点![]() 和
和![]() 关于
关于![]() 对称 ,当
对称 ,当![]() 与
与![]() 重合时,
重合时,![]() 为
为![]() 的延长线上满足
的延长线上满足![]() 的点,当
的点,当![]() 与
与![]() 不重合时,
不重合时,![]() 为
为![]() 的延长线与过
的延长线与过![]() 且垂直于
且垂直于![]() 的直线的交点,
的直线的交点,
(1)当![]() 与
与![]() 不重合时,
不重合时,![]() 的结论是否成立?试证明你的判断.
的结论是否成立?试证明你的判断.
(2)设![]() 求
求![]() 关于
关于![]() 的函数及其定义域;
的函数及其定义域;
(3)如存在![]() 或
或![]() 恰好落在弧
恰好落在弧![]() 或弧
或弧![]() 上时,求出此时
上时,求出此时![]() 的值;如不存在,则请说明理由.
的值;如不存在,则请说明理由.
(4)请直接写出当![]() 从
从![]() 运动到
运动到![]() 时,线段
时,线段![]() 扫过的面积.
扫过的面积.
【答案】(1)成立;(2)![]() ;(3)x=0或x=2;(4)
;(3)x=0或x=2;(4)![]()
【解析】
试题分析:(1)设DE交AC于M,DF交BC于N.由轴对称图形的性质可知EM=DM,ED⊥AC,然后可证明AC∥DF,由平行线分线成比例定理可知 ;
(2)①当D与A不重合时.先证明四边形CNDM是矩形,从而得到MD∥BC,由平行线的性质可知∠ADM=∠ABC=30°,由特殊锐角三角函数可知ED=![]() ,DN=
,DN=![]() =
= ![]() (4﹣x)=2﹣
(4﹣x)=2﹣![]() ,然后由平行线分线段成比例定理可知DN=NF,从而得到DF=2DN=4﹣x,最后在Rt△EFD中,由勾股定理可求得y与x的函数关系式;②当D与A重合时,y=2AC=4;
,然后由平行线分线段成比例定理可知DN=NF,从而得到DF=2DN=4﹣x,最后在Rt△EFD中,由勾股定理可求得y与x的函数关系式;②当D与A重合时,y=2AC=4;
(3)①当点E在弧AC上时.由题意可知∠CAD=60°,由点E与点D关于AC对称可知:∠EAD=120°,故此点E不在弧AC上,故当且仅当点D与点A重合是,点E也与点A重合时,成立;②当点F在 上时,如图3所示,连接BF、AF.由题意可知∠FDB=60°,由(2)可知DF=2DN,DB=2DN,故此DF=DB,从而可证明△DFB为等边三角形,于是得到DB=DF,然后再证明AD=DF,从而可知点D与点O重合,于是得到AD= =2;
(4)由(2)可知∠EAD=2∠CAD=120°,故此点E运动的轨迹为一条线段,由(3)可知∠FBD=60°,故此点F运动的轨迹也是一条线段,然后画出图形,最后利用三角形的面积公式即可求得答案.
试题解析:
成立:如图,设DE交AC于M,DF交BC于N;
由已知,![]() ,
,![]()
故![]() ,因此
,因此![]() ,又
,又![]() ,
,![]() .
.
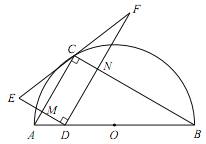
当D与A不重合时,![]() ,由AD=x,
,由AD=x,
得![]() 中,
中,![]() ,故
,故![]() ;
;
![]() 中,BD=4-x,故
中,BD=4-x,故![]() ,
,
由(1),![]() ,故
,故![]() ,因此DF=4-x=DB;
,因此DF=4-x=DB;
![]() 中,
中,![]() ;
;
当D与A重合时,如图A、D、E重合,故y=EF=2AC=4(x=0);

综上,![]() ;
;
当E在![]() 上时,由翻折的性质,
上时,由翻折的性质,![]() ,
,
而此时![]() ,不满足条件,
,不满足条件,
故当且仅当D与A重合时,E也与A重合符合条件,此时AD=0;
当F在![]() 上时,如图,连接BF、AF,
上时,如图,连接BF、AF,
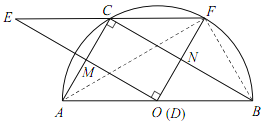
由![]() 且DF=DB,故
且DF=DB,故![]() 为等边三角形,
为等边三角形,![]() ,
,
AB为直径,故![]() ,
,![]() ,
,
因此AD=FD=BD,即此时D与O重合,DF=2;
又此时DF=4-x=2,故x=2;
综上,x=0或x=2;
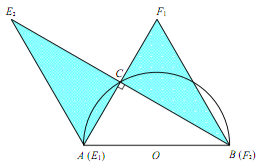
如图,EF初始位置为![]() ,
,![]() 与A点重合;
与A点重合;
EF终止位置为![]() ,
,![]() 与B点重合;
与B点重合;
由![]() ,故知E点运动轨迹为线段
,故知E点运动轨迹为线段![]() ;
;
![]() ,故知F点运动轨迹为线段
,故知F点运动轨迹为线段![]() ,
,
阴影部分面积即为所求,![]() .
.

 阅读快车系列答案
阅读快车系列答案