ЬтФПФкШн
ЁОЬтФПЁПзлКЯгыЬНОПЃКШчЭМЃЌвбжЊХзЮяЯпyЃНЃx2ЃЋbxЃЋcгывЛжБЯпЯрНЛгкA(Ѓ1ЃЌ0)ЃЌC (2ЃЌ3)СНЕуЃЌгыyжсНЛгкЕуNЃЌЦфЖЅЕуЮЊD ЁЃ
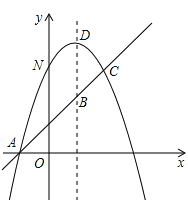
ЃЈ1ЃЉШЗЖЈХзЮяЯпМАжБЯпACЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕуMдкжБЯпx =3ЩЯЃЌЧѓЪЙ MNЃЋMD ЕФжЕзюаЁЪБЕФMЕузјБъЃЛ
ЃЈ3ЃЉШєХзЮяЯпЕФЖдГЦжсгыжБЯпAC ЯрНЛгкЕуBЃЌE ЮЊжБЯпAC ЩЯЕФШЮвтвЛЕуЃЌЙ§ЕуE зїEFЁЮBD НЛХзЮяЯпгкЕуFЃЌвдBЁЂDЁЂEЁЂF ЮЊЖЅЕуЕФЫФБпаЮФмЗёЮЊЦНааЫФБпаЮЃПШєФмЃЌЧѓЕуE ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЁЃ
ЁОД№АИЁПЃЈ1ЃЉy=-x2+2x+3ЃЌжБЯпACЮЊy=x+1ЃЎЃЈ2ЃЉMЃЈ3ЃЌ![]() ЃЉЃЛЃЈ3ЃЉEЃЈ0ЃЌ1ЃЉЛђЃЈ
ЃЉЃЛЃЈ3ЃЉEЃЈ0ЃЌ1ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉНЋЕуAЁЂCЕФзјБъДњШыХзЮяЯпНтЮіЪНПЩЕУГіbЁЂcЕФжЕЃЌМЬЖјЕУГіХзЮяЯпНтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіACЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉРћгУжсЖдГЦЧѓзюЖЬТЗОЖЕФжЊЪЖЃЌевЕНNЕуЙигкжБЯпx=3ЕФЖдГЦЕуNЁфЃЌСЌНгN'DЃЌN'DгыжБЯпx=3ЕФНЛЕуМДЪЧЕуMЕФЮЛжУЃЌМЬЖјЧѓГіmЕФжЕЃЎ
ЃЈ3ЃЉЩшГіЕуEЕФзјБъЃЌЗжЧщПіЬжТлЃЌЂйЕБЕуEдкЯпЖЮACЩЯЪБЃЌЕуFдкЕуEЩЯЗНЃЌЂкЕБЕуEдкЯпЖЮACЃЈЛђCAЃЉбгГЄЯпЩЯЪБЃЌЕуFдкЕуEЯТЗНЃЌИљОнЦНааЫФБпаЮЕФаджЪБэЪОГіFЕФзјБъЃЌНЋЕуFЕФзјБъДњШыХзЮяЯпНтЮіЪНПЩЕУГіxЕФжЕЃЌМЬЖјЧѓГіЕуEЕФзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩХзЮяЯпy=-x2+bx+cЙ§ЕуAЃЈ-1ЃЌ0ЃЉМАCЃЈ2ЃЌ3ЃЉЃЌПЩЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЮЊy=-x2+2x+3ЃЌ
ЩшжБЯпACНтЮіЪНЮЊy=kx+nЃЌНЋЕуAЃЈ-1ЃЌ0ЃЉЁЂCЃЈ2ЃЌ3ЃЉДњШыЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЙЪжБЯпACЮЊy=x+1ЃЎ
ЃЈ2ЃЉзїNЕуЙигкжБЯпx=3ЕФЖдГЦЕуNЁфЃЌдђNЁфЃЈ6ЃЌ3ЃЉЃЌгЩЃЈ1ЃЉЕУDЃЈ1ЃЌ4ЃЉЃЌ
ПЩЧѓГіжБЯпDNЁфЕФКЏЪ§ЙиЯЕЪНЮЊy=-![]() x+
x+![]() ЃЌ
ЃЌ
ЕБMЃЈ3ЃЌmЃЉдкжБЯпDNЁфЩЯЪБЃЌMN+MDЕФжЕзюаЁЃЌ
дђm=-![]() ЁС3+
ЁС3+![]() =
=![]() ЃЎ
ЃЎ
ЁрMЃЈ3ЃЌ![]() ЃЉ
ЃЉ
ЃЈ3ЃЉгЩЃЈ1ЃЉЁЂЃЈ2ЃЉЕУDЃЈ1ЃЌ4ЃЉЃЌBЃЈ1ЃЌ2ЃЉ
ЕуEдкжБЯпACЩЯЃЌЩшEЃЈxЃЌx+1ЃЉЃЌ
ЂйЕБЕуEдкЯпЖЮACЩЯЪБЃЌЕуFдкЕуEЩЯЗНЃЌдђFЃЈxЃЌx+3ЃЉЃЌ
ЁпFдкХзЮяЯпЩЯЃЌ
Ёрx+3=-x2+2x+3
НтЕУЃЌx=0Лђx=1ЃЈЩсШЅЃЉЃЌ
дђЕуEЕФзјБъЮЊЃКЃЈ0ЃЌ1ЃЉЃЎ
ЂкЕБЕуEдкЯпЖЮACЃЈЛђCAЃЉбгГЄЯпЩЯЪБЃЌЕуFдкЕуEЯТЗНЃЌдђFЃЈxЃЌx-1ЃЉЃЌ
ЁпЕуFдкХзЮяЯпЩЯЃЌ
Ёрx-1=-x2+2x+3ЃЌ
НтЕУx=![]() Лђx=
Лђx=![]() ЃЌ
ЃЌ
МДЕуEЕФзјБъЮЊЃКЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
злЩЯПЩЕУТњзуЬѕМўЕФЕуEЮЊEЃЈ0ЃЌ1ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ