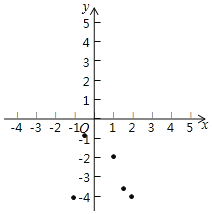题目内容
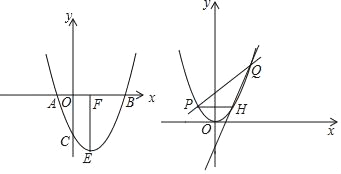
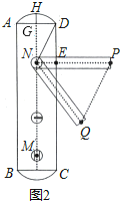
【题目】小明家的门框上装有一把防盗门锁（如图1），其平面结构图如图2所示，锁身可以看成由两条等弧
，
和矩形
组成的，的圆心是倒锁按钮点
．已知的弓形高
，
，
．当锁柄
绕着点
顺时针旋转至
位置时，门锁打开，此时直线
与所在的圆相切，且
，
．
（1）求所在圆的半径；
（2）求线段
的长度．（
，结果精确到
）
【答案】（1）即
所在圆的半径为
；（2）
cm．
【解析】
（1）连结
，设
交
于点
，设
，在
中，根据勾股定理，列方程，即可求解；
（2）延长
交
的延长线于点
，设直线与所在的圆相切于点
，连结
．由
，
得
，结合
，
cm，
cm，由
，得
，
，进而得
，即可求解．
（1）如图，连结，设交于点．
∴BK=AG=
,
设，
∴在中，
，
解得：
，
即所在圆的半径为；
（2）如图，延长交的延长线于点，设直线与所在的圆相切于点，连结．
，
．
，
，
，
．
cm，
cm，
cm．
直线与所在的圆相切于点，
，
cm，
，
，
，
，
，
cm，
，
．
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”，公交公司积极响应将旧车换成节能环保公交车，计划购买A型和B型两种环保型公交车10辆，其中每台的价格、年载客量如表：
A型 | B型 | |
价格（万元/台） | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆，B型环保公交车2辆，共需400万元；若购买A型环保公交车2辆，B型环保公交车1辆，共需350万元．
（1）求x、y的值；
（2）如果该公司购买A型和B型公交车的总费用不超过1200万元，且确保10辆公交车在该线路的年载客量总和不少于680万人次，问有哪几种购买方案？
（3）在（2）的条件下，哪种方案使得购车总费用最少？最少费用是多少万元？
【题目】小浩根据学习函数的经验，对函数
的图像和性质进行深入探究，过程如下，请补充完整．
自变量
的取值范围是全体实数，与
的几组对应数值如下表：
| … |
|
|
|
|
| 0 | 0．5 | 1 | 1．5 | 2 |
| … |
| … |
|
|
|
|
| 0 |
|
|
|
| 0 | … |
表中
的值是_______．
（2）如图，在平面直角坐标系
中，描出了以上表中部分对应值为坐标的点，根据描出的点，画出该函数的图像．
（3）类比抛物线
，试从图像的轴对称性、增减性、有无最值三个方面分别说明函数具有的性质：（各写一条即可）
___________________________________________________________________________
（4）进一步探究函数图像发现：
①函数图像与轴有_______个交点，所以对应的方程
有______个实数根；
②方程
有_______个实数根；
③对关于的方程
，模仿②写出一个真命题．
____________________________________________________________
