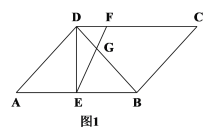
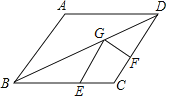
[题目]如图.菱形ABCD中.AB＝4.∠ABC＝60°.点E.F.G分别为线段BC.CD.BD上的任意一点.则EG+FG的最小值为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，菱形ABCD中，AB＝4，∠ABC＝60°，点E、F、G分别为线段BC，CD，BD上的任意一点，则EG+FG的最小值为______．

【答案】2

【解析】

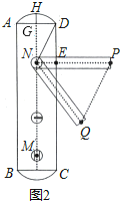
根据轴对称确定最短路线问题，作点E关于BD的对称点E′，连接E′F与BD的交点即为所求的点G，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知E′F⊥CD时EG+FG的最小值，然后求解即可．

如图，作CK⊥AB于K，E关于BD的对称点E′，作E′H⊥CD于H，当E′、G、F共线，点F与H重合时，EG+GF的值最小，最小值为E′H的长，即CK的长，

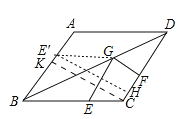
∵四边形ABCD为菱形，AB＝4，

∴BC=4，

∵∠ABC＝60°，

∴CK=4×＝2，

∴EG+FG的最小值为2．

故答案为：2．

练习册系列答案

开心15天精彩寒假巧计划江苏凤凰科学技术出版社系列答案

（1）求证：BE=CF.

（2）当四边形ACDE为菱形时，求BD的长.

【题目】如图，线段AB绕着点A逆时针方向旋转120°得到线段AC，点B对应点C，在∠BAC的内部有一点P，PA＝8，PB＝4，PC＝4，则线段AB的长为_____．

【题目】将一副三角尺按如图①方式拼接：含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合（在Rt△ABC中，∠ACB＝90°，∠BAC＝30°；在Rt△ACD中，∠ADC＝90°∠DAC＝45°）已知AB＝2，P是AC上的一个动点．

（1）当PD＝BC时，求∠PDA的度数；

（2）如图②，若E是CD的中点，求△DEP周长的最小值；

（3）如图③，当DP平分∠ADC时，在△ABC内存在一点Q，使得∠DQC＝∠DPC，且CQ＝，求PQ的长．

【题目】小明家的门框上装有一把防盗门锁（如图1），其平面结构图如图2所示，锁身可以看成由两条等弧，和矩形组成的，的圆心是倒锁按钮点．已知的弓形高，，．当锁柄绕着点顺时针旋转至位置时，门锁打开，此时直线与所在的圆相切，且，．

（1）求所在圆的半径；

（2）求线段的长度．（，结果精确到）

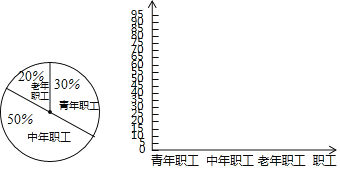
【题目】某单位有职工200人，其中青年职工（20﹣35岁），中年职工（35﹣50岁），老年职工（50岁及以上）所占比例如扇形统计图所示．

为了解该单位职工的健康情况，小张、小王和小李各自对单位职工进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．

表1：小张抽样调查单位3名职工的健康指数

年龄	26	42	57
健康指数	97	79	72

表2：小王抽样调查单位10名职工的健康指数

年龄	23	25	26	32	33	37	39	42	48	52
健康指数	93	89	90	83	79	75	80	69	68	60

表3：小李抽样调查单位10名职工的健康指数

年龄	22	29	31	36	39	40	43	46	51	55
健康指数	94	90	88	85	82	78	72	76	62	60

根据上述材料回答问题：

（1）小张、小王和小李三人中，谁的抽样调查的数据能够较好地反映出该单位职工健康情况，并简要说明其他两位同学抽样调查的不足之处．

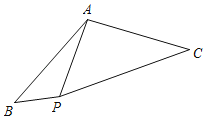
（2）根据能够较好地反映出该单位职工健康情况表，绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图．

【题目】如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线交AB，BC分别于点M，N，反比例函数的图象经过点M，N．

（1）求反比例函数的解析式；

（2）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．

【题目】在平行四边形ABCD中，AD=BD，E为AB的中点，F为CD上一点，连接EF交BD于G．

（1）如图1，若DF=DG=2，AB=8，求EF的长；

（2）如图2，∠ADB=90°，点P为平行四边形ABCD外部一点，且AP=AD，连接BP、DP、EP，DP交EF于点Q，若BP⊥DP，EF⊥EP，求证：DQ=PQ．

【题目】“村村通公路政策，是近年来国家构建和谐社会，支持新农村建设的一项重大公共决策，是一项民心工程，惠民工程某镇政府准备向甲、乙两个工程队发包一段“村村通”工程建设项目，经调查：甲、乙两队单独完成该工程，乙队所需时间是甲队的2倍；甲、乙两队共同完成该工程需30天；若甲队每天所需劳务费用为2400元，乙队每天所需劳务费用为1500元，从节约资金的角度考虑，应选择哪个工程队更合算？

试题分类