题目内容
【题目】已知一次函数 y1=k1x与![]() 的图象都经过点(2,2).
的图象都经过点(2,2).
(1)填空:k1= ,k2= ;
(2)在同一坐标系中作出这两个函数的图象;
(3)直接写出当y1>y2时,自变量x的取值范围: .
【答案】(1)1,4;(2)见解析;(3)﹣2<x<0或x>2.
【解析】
(1)把点(2,2)的坐标分别代入两函数的解析式,即可求出答案;
(2)根据两函数的解析式画出图象即可;
(3)求出两函数的图象的交点坐标,结合图象即可得出答案.
(1)把点(2,2)代入 y1=k1x得:2=2k1,
解得:k1=1,
点(2,2)代入![]() 得:2=
得:2=![]() ,
,
解得:k2=4,
故答案为:1,4;
(2)两函数的解析式是y1=x,y2=![]() ,
,
过点(0,0)和点(2,2)的直线,就是函数y1=x的图象,
|
| -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 |
|
|
| -0.8 | -1 | -1.33 | -2 | -4 | 4 | 2 | 1.33 | 1 | 0.8 |
|
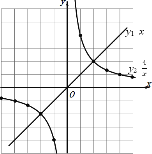
描点,连线,它们的图象如图所示:
 ;
;
(3)∵解方程组![]() 得:
得: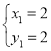 ,
,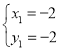 ,
,
∴两函数的交点坐标是(2,2)、(﹣2,﹣2),
∴当y1>y2时,自变量x的取值范围是﹣2<x<0或x>2,
故答案为:﹣2<x<0或x>2.

练习册系列答案
相关题目