题目内容
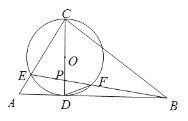
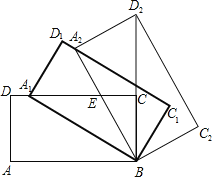
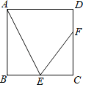
【题目】如图,正方形ABCD,点E为BC中点,点F在边CD上,连接AE、EF,若∠FEC=2∠BAE,CF=8,则线段AE的长为_____.
【答案】![]()
【解析】
根据题意连接AF,过点A作AM⊥EF,设∠BAE=α,则∠FEC=2α,根据全等三角形的性质得到DF=MF,同理EM=BE,设DF=a,则CD=8+a,由点E为BC边上的中点,得到BE=EC=EM=![]() a+4,求得EF=
a+4,求得EF=![]() a+4,根据勾股定理列方程即可得到结论.
a+4,根据勾股定理列方程即可得到结论.
解:连接AF,过点A作AM⊥EF,如图所示,

∵∠FEC=2∠BAE,
设∠BAE=α,则∠FEC=2α,
∴∠BEA=90°﹣α,
∴∠AEM=90﹣α,
∴∠AEB=∠AEM,
∵AB⊥BE,AM⊥EM,
∴AB=AM=AD,
∵AF=AF,
∴Rt△AMF≌Rt△ADF(HL),
∴DF=MF,
同理EM=BE,
设DF=a,则CD=8+a,
点E为BC边上的中点,
∴BE=EC=EM=![]() a+4,
a+4,
∴EF=![]() a+4,
a+4,
∴(![]() a+4)2+82=(
a+4)2+82=(![]() a+4)2,
a+4)2,
解得a=4(负值舍去),
∴DF=4,
∴AB=12,BE=6,
∴AE=![]() =6
=6![]() ,
,
故答案为:6![]() .
.

【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.

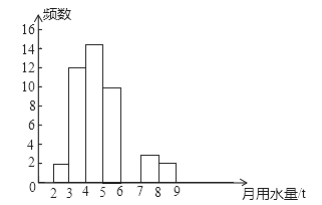
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.