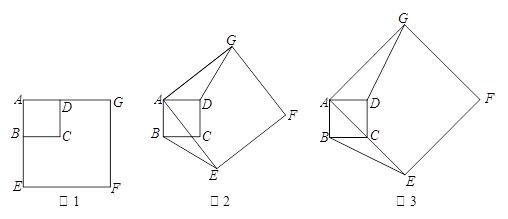题目内容
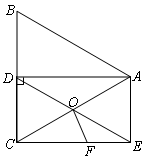
如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为 的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为
 的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
(1)证明见解析;(2) .
.
 .
.试题分析:(1)根据平行四边形判定得出平行四边形,再根据矩形判定推出即可.
(2)分别求出AE、OH、CE、CF的长,再求出三角形AEC和三角形COF的面积,即可求出答案.
试题解析:(1)∵CE∥AD且CE=AD,∴四边形ADCE是平行四边形.
∵AD⊥BC,∴∠ADC=90°.
∴四边形ADCE是矩形.
(2)∵△ABC是等边三角形,边长为4,∴AC=4,∠DAC=30°.
∴∠ACE=30°,AE=2,CE=
 .
.∵四边形ADCE为矩形,∴OC=OA=2.
∵CF=CO,∴CF=2.
如图,过O作OH⊥CE于H,
∴OE=
 OC=1.
OC=1.∴
 .
.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线 ,连接
,连接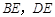 ,其中
,其中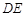 交直线
交直线 .
. ,求
,求 的度数;
的度数; ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.

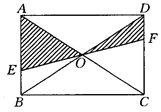
 . 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
. 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG. ,求点G到BE的距离.
,求点G到BE的距离.