题目内容
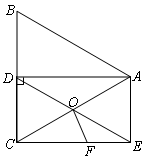
如图，在?ABCD中，∠ABC=5∠A，过点B作BE⊥DC交AD的延长线于点E，O是垂足，且DE=DA=4cm，
求：（1）?ABCD的周长；
（2）四边形BDEC的周长和面积（结果可保留根号）
求：（1）?ABCD的周长；
（2）四边形BDEC的周长和面积（结果可保留根号）
（1）∵∠ABC=5∠A，∠ABC+∠A=180°，
∴∠A=30°，
又∵AE=AD+DE=8cm，
∴AB=AEcos∠A=4
cm，BE=AEsin∠A=4cm，
故可得?ABCD的周长=2（AD+AB）=（8+8
）cm．
（2）∵点D是AE的中点，∠ABE是直角，
∴BD=DE=AD，
又∵四边形BDEC是平行四边形，
∴四边形BDEC是菱形，
故四边形BDEC的周长=4DE=16cm；面积=
DC•BE=8
cm2．
∴∠A=30°，
又∵AE=AD+DE=8cm，
∴AB=AEcos∠A=4
| 3 |
故可得?ABCD的周长=2（AD+AB）=（8+8
| 3 |
（2）∵点D是AE的中点，∠ABE是直角，
∴BD=DE=AD，
又∵四边形BDEC是平行四边形，
∴四边形BDEC是菱形，
故四边形BDEC的周长=4DE=16cm；面积=
| 1 |
| 2 |
| 3 |
练习册系列答案
手拉手全优练考卷系列答案
相关题目
的等边三角形，AC，DE相交于点O，在CE上截取CF=CO，连接OF，求线段FC的长及四边形AOFE的面积.
