题目内容
【题目】如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′，若AB＝8，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是（ ）
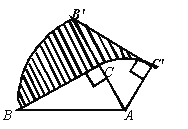
A. 8π B. 6π C. 4π D. 2π
【答案】A
【解析】分析: 根据阴影部分的面积是：扇形BAB′的面积+S△AB′C′-S△ABC-扇形CAC′的面积，分别求得：扇形BAB′的面积S△AB′C′，S△ABC以及扇形CAC′的面积，即可求解.
详解: 扇形BAB′的面积是： 
= 
，
在直角△ABC中，BC=ABsin60°=8×
=4
，AC=
AB=4，
S△ABC=S△AB′C′=ACBC=×4×4=16．
扇形CAC′的面积是：
=
，
则阴影部分的面积是：扇形BAB′的面积+S△AB′C′-S△ABC-扇形CAC′的面积
=- =8π．
故选：A.
点睛: 本题考查了扇形的面积的计算，正确理解阴影部分的面积是：扇形BAB′的面积+S△AB′C′-S△ABC-扇形CAC′的面积是关键．
练习册系列答案
相关题目
【题目】为了解高中学生每月用掉中性笔笔芯的情况，随机抽查了30名高中学生进行调查，并将调查的数据制成如下的表格：
月平均用中性笔笔芯(根) | 4 | 5 | 6 | 7 | 8 | 9 |
被调查的学生数 | 7 | 4 | 9 | 5 | 2 | 3 |
请根据以上信息，解答下列问题：
(1)被调查的学生月平均用中性笔笔芯数大约________根；
(2)被调查的学生月用中性笔笔芯数的中位数为________根，众数为________根；
(3)根据样本数据，若被调查的高中共有1000名学生，试估计该校月平均用中性笔笔芯数9根的约多少人？
