题目内容
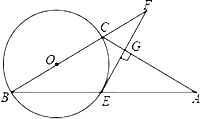
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
【答案】(1)证明见解析;(2)CG=![]() .
.
【解析】分析: (1)证明OE是△ABC的中位线,得出OE∥AC,再由已知条件得出FE⊥OE,即可得出结论;
(2)由切割线定理求出直径,得出半径的长,由平行线得出三角形相似,得出比例式,即可得出结果.
详解:
(1)证明:连接CE,
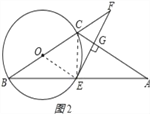
∵BC是直径,
∴∠BEC=90°,
∴CE⊥AB;
又∵AC=BC,
∴AE=BE.
连接OE,
∵BE=AE,OB=OC,
∴OE是△ABC的中位线,
∴OE∥AC,AC=2OE=6.
又∵EG⊥AC,
∴FE⊥OE,
∴FE是⊙O的切线.
(2)∵EF是⊙O的切线,∠CEF+∠CEO=900,且BC是直径
∴∠BEO+∠CEO=900
∴∠CEF=∠BEO,∠F为公共角,
∴ΔCEF∽ΔEBF
∴FE2=FCFB.
设FC=x,则有2FB=16,
∴FB=8,
∴BC=FB﹣FC=8﹣2=6,
∴OB=OC=3,即⊙O的半径为3;
∴OE=3,
∵OE∥AC,
∴△FCG∽△FOE,
∴![]() ,即
,即![]() ,
,
解得:CG=![]() .
.
点睛: 本题考查了切线的判定、等腰三角形的性质、三角形中位线的判定、切割线定理、相似三角形的判定与性质;熟练掌握切线的判定,由三角形中位线定理得出OE∥AC是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案【题目】某公司改革实行每月考核再奖励的新制度,大大调动了员工的积极性,![]() 年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
年一名员工每月奖金的变化如下表:(正数表示比前一月多的钱数,负数表示比前一月少的钱数)单位:(元)
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
钱数变化 |
|
|
|
|
|
|
|
(1)若![]() 年底
年底![]() 月份奖金为
月份奖金为![]() 元,用代数式表示
元,用代数式表示![]() 年二月的奖金;
年二月的奖金;
(2)请判断七个月以来这名员工得到奖金最多是哪个月?最少是哪个月?他们相差多少元?
(3)若![]() 年这七个月中这名员工最多得到的奖金是
年这七个月中这名员工最多得到的奖金是![]() 元,请问
元,请问![]() 年
年![]() 月份他得到多少奖金?
月份他得到多少奖金?