题目内容
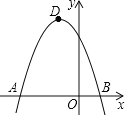
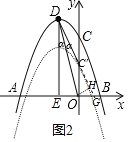
【题目】在平面直角坐标系中,二次函数y=-x2-bx+c的图象经过点A,点B(1,0)和点C(0,3).点D是抛物线的顶点.
(1)求二次函数的解析式和点D的坐标
(2)直线y=kx+n(k≠0)与抛物线交于点M,N,当△CMN的面积被y轴平分时,求k和n应满足的条件
(3)抛物线的对称轴与x轴交于点E,将抛物线向下平移m(m>0)个单位,平移后抛物线与y轴交于点C′,连接DC′,OD,是否存在OD平分∠C′DE的情况?若存在,求出m的值;若不荐在,请说明理由.
【答案】(1)y=-x2-2x+3,点D(-1,4);(2)k=-2,n<3;(3)存在,m=![]() .
.
【解析】
(1)利用待定系数法求得解析式,利用二次函数的顶点坐标公式即可求得点D的坐标;
(2)联立直线与抛物线的解析式得出关于x的一元二次方程,根据要使y轴平分△CMN的面积,则M、N两点的横坐标互为相反数,根据根与系数的关系即可得出k值;再根据而点H在点C之下这一条件,可得出n的取值范围;
(3)解答本类题目的总体思路在于先假设存在,若能求出m的值则假设成立,否则不成立;若存在,首先根据角平分线的性质,得出OH= 1,DH= 4;进而设HG=a,由△DOG的面积建立关于a的方程组,解之可得点G的坐标,进而求出直线DG的表达式和OC′,与OC作差,即可求出m的值,说明存在OD平分∠C′DE的情况.
(1)y=-x2-bx+c=-x2-bx+3,将点B坐标代入上式得:0=-1-b+3,
解得:b=2,
故抛物线的表达式为:y=-x2-2x+3,
则点A(-3,0)、点D(-1,4);
(2)设点M、N的横坐标为x1、x2,
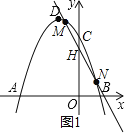
当△CMN的面积被y轴平分时,则x1+x2=0,
将二次函数表达式与直线表达式联立并整理得:
x2+(2+k)x+(n-3)=0,
x1+x2=-(2+k)=0,即k=-2,
而点H在点C之下,故n<3,
故:k=-2,n<3;
(3)存在,理由:
OD平分∠C′DE,即:∠EDO=∠ODC′,
延长DC′交x轴于点G,过点O作OH⊥DG交于H,
∵∠EDO=∠ODC′,
∴OH=OE=1,DH=DE=4,
设HG=a,则OG=![]() ,
,
S△DOG=![]() OG×DE=
OG×DE=![]() OH×GD,
OH×GD,
即:4![]() =1×(4+a),
=1×(4+a),
解得:a=![]() ,即点G(
,即点G(![]() ,0),
,0),
∴直线DG的表达式为:y=-![]() x+
x+![]() ,
,
即OC′=![]() ,
,
m=3-![]() =
=![]() .
.