Question

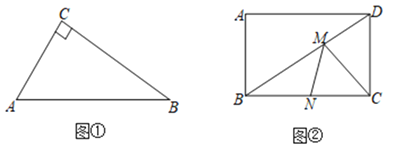
【题目】（1）如图①，Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D是AB边上任意一点，则CD的最小值为____．

（2）如图②，矩形ABCD中，AB＝3，BC＝4，点M、点N分别在BD、BC上，求CM+MN的最小值____．

Answer 1

【答案】

【解析】

（1）先利用点到直线的距离确定CD最小时点D位置，再用三角形的面积求出CD的长；

（2）先根据轴对称确定出点M和N的位置，再利用面积求出CF，进而求出CE，最后用三角函数即可求出CM+MN的最小值．

（1）解：如图①，过点C作CD⊥AB于D，

根据点到直线的距离垂线段最短，此时CD最小，

在Rt△ABC中，AC=3，BC=4，根据勾股定理得，AB=5

∵

∴

（2）如图②，作出点C关于BD的对称点E,

过点E作EN⊥BC于N，交BD于M，连接CM，此时CM + MN= EN最小；

∵四边形ABCD是矩形，

∴∠BCD=90°，CD=AB=3，

∵BC＝4，

根据勾股定理得，BD=5，
∵CE⊥BC，

∴

∴CF=

由对称得，CE=2CF=

在Rt△BCF中，cos∠BCF=，

∴sin∠BCF=

在Rt△CEN中，EN=CE·sin∠BCF=；

即：CM+MN的最小值为：