Question

【题目】已知∠PAQ=36°，点B为射线AQ上一固定点，按以下步骤作图：①分别以A，B为圆心，大于AB的长为半径画弧，相交于两点M，N；②作直线MN交射线AP 于点D，连接 BD；③以B为圆心，BA长为半径画弧，交射线AP 于点C； 根据以上作图过程及所作图形，下列结论中错误的是（ ）

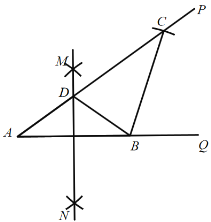
A.∠CDB=72°B.△ADB∽△ABCC.CD：AD=2：1D.∠ABC=3∠ACB

Answer 1

【答案】C

【解析】

根据垂直平分线的性质、等腰三角形的性质及判定，相似三角形的判定一一判断即可．

解：由作图可知，MN垂直平分AB，AB＝BC，

∵MN垂直平分AB，

∴DA＝DB，

∴∠A＝∠DBA，

∵∠PAQ＝36°，

∴∠CDB＝∠A＋∠DBA＝72°，（A正确）

∵AB＝BC，

∴∠A＝∠ACB＝36°，

∴∠ABD＝∠ACB，

又∵∠A＝∠A，

∴△ADB∽△ABC，（B正确）

∵∠A＝∠ACB＝36°，

∴∠ABC＝180°－∠A－∠ACB＝108°，

∴∠ABC＝3∠ACB，（D正确）

∵∠ABD＝36°，∠ABC＝108°，

∴∠CBD＝∠ABC－∠ABD＝72°，

∴∠CBD＝∠CDB＝72°，

∴CD＝BC，

∵∠A＝∠ACB＝36°，

∴AB＝BC，

∴CD＝AB，

∵AD＋DB＞AB，AD＝DB

∴2AD＞AB

∴2AD＞CD，（C错误）

故选：C