Question

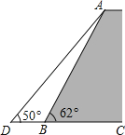
【题目】如图，某防洪堤坝长300米，其背水坡的坡角∠ABC=62°，坡面长度AB=25米（图为横截面），为了使堤坝更加牢固，一施工队欲改变堤坝的坡面，使得加固后坡面的坡角∠ADB=50°

（1）求此时应将坝底向外拓宽多少米？（结果保留到0.01米）

（2）完成这项工程需要土石多少立方米？（参考数据：sin62°≈0.88，cos62°≈0.47，tan50°≈1.20）

Answer 1

【答案】（1）应将坝底向外拓宽大约6.58米；（2）21714立方米

【解析】

（1）过A点作AE⊥CD于E．在Rt△ABE中，根据三角函数可得AE，BE，在Rt△ADE中，根据三角函数可得DE，再根据DB=DE-BE即可求解；

（2）用△ABD的面积乘以坝长即为所需的土石的体积．

解：（1）过A点作AE⊥CD于E．

在Rt△ABE中，∠ABE=62°．

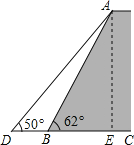
∴AE=ABsin62°≈25×0.88=22米，

BE=ABcos62°≈25×0.47=11.75米，

在Rt△ADE中，∠ADB=50°，

∴DE==18.33米，

∴DB=DE-BE≈6.58米．

故此时应将坝底向外拓宽大约6.58米．

（2）6.58×22××300=21714立方米．