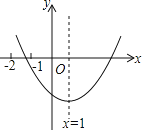题目内容
【题目】已知抛物线
：
和抛物线
：
，其中
．
下列说法你认为正确的序号是______；
抛物线和与y轴交于同一点
；
抛物线和开口都向上；
抛物线和的对称轴是同一条直线；
当
时，抛物线和都与x轴有两个交点
抛物线和相交于点E、F，当k的值发生变化时，请判断线段EF的长度是否发生变化，并说明理由；
在中，若抛物线的顶点为M，抛物线的顶点为N，问：
是否存在实数k，使
？如存在，求出实数k；如不存在，请说明理由．
【答案】（1）①③④；（2）
；（3）
【解析】
（1）①分别把
代入即可；
②根据二次项系数进行判断；
③抛物线的对称轴是：
，代入计算即可；
④根据△
来判断；
（2）由对称性可知：两条抛物线相交的另一个交点
与点
的纵坐标相等，由
得：
，则
就等于
，所以线段
；
（3）存在实数
，使
，利用配方法分别求
、
的坐标，根据两点的距离得：
的长，利用解方程即可．
解：
抛物线
：
经过
，抛物线
：
经过，
抛物线和与y轴交于同一点
；
所以
结论正确；
抛物线：
，则抛物线开口向下，
抛物线：k不确定为正数或负数，则抛物线的开口也不确定；
所以结论不正确；
抛物线：对称轴为直线：
，
抛物线：对称轴为直线：
，
抛物线和的对称轴是同一条直线；
所以结论正确；
抛物线：，
，
当
时，
，所以抛物线与x轴有两个交点，
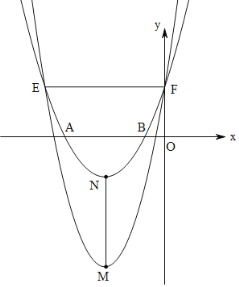
抛物线：，
，
当时，，所以抛物线与x轴有两个交点，
所以当时，抛物线和都与x轴有两个交点，
所以结论正确；
故说法正确的序号是：
；
故答案为：；
注：每个正确选项得1分，选错不得分。
由
可知：点是抛物线和与y轴一个交点，
两条抛物线相交的另一个交点E与点F的纵坐标相等，
当
时，二次函数和重合，
当
时，k的值变化时，线段EF的长不会变化，
理由是：
抛物线和的对称轴是同一条直线：直线
，又；
点F关于直线对称的点E的坐标为
，
则EF就等于
，
所以线段
；
存在实数k，使
，
，
抛物线，顶点
，
抛物线，顶点
，
由题意得：
，
解得：．
