题目内容
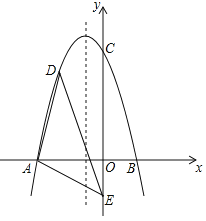
【题目】如图,△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD折叠,使点C落在点F处,线段DF与AB相交于点E.
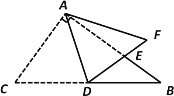
(1)求∠BDE的度数.
(2)求证:△DEB∽△ADB.
(3)若BC=4,求BE的长.
【答案】(1)36°;(2)详见解析;(3)![]()
【解析】
(1)根据三角形内角和定理求出∠C=90°-∠B=54°.由直角三角形斜边上的中线的性质得出AD=BD=CD,利用等腰三角形的性质求出∠BAD=∠B=36°,∠DAC=∠C=54°,利用三角形内角和定理求出∠ADC=180°-∠DAC-∠C=72°.再根据折叠的性质得出∠ADF=∠ADC=72°,然后根据平角的定义得出∠BDE=180°-∠ADC-∠ADF=36°.
(2)根据∠B=∠B,∠BDE=∠BAD证明即可;
(3)由△DEB∽△ADB得![]() ,设BE=x得方程x(x+2)=4,求解方程即可.
,设BE=x得方程x(x+2)=4,求解方程即可.
(1)∵在Rt△ABC中,∠BAC=90°,∠B=36°,
∴∠C=90°-∠B=54°.
∵AD是斜边BC上的中线,
∴AD=BD=CD,
∴∠BAD=∠B=36°,∠DAC=∠C=54°,
∴∠ADC=180°-∠DAC-∠C=72°.
∵将△ACD沿AD对折,使点C落在点F处,
∴∠ADF=∠ADC=72°,
∴∠BDE=180°-∠ADC-∠ADF=180°-72°-72°=36°.
(2)∵∠BAC=90°,AD是斜边BC上的中线,
∴AD=BD,
∵∠B=36°,∴∠BAD=36°,
∵∠BDE=36°,
∴∠B=∠B,∠BDE=∠BAD,
∴△DEB∽△ADB.
(3)∵△DEB∽△ADB,
∴![]() ,设BE=x,
,设BE=x,
∵BC=4,
∴![]() ,
,
∴BE=x=![]()

练习册系列答案
相关题目