Question

【题目】已知二次函数，它的图象经过点．

若该图象与轴的一个交点为．

①求二次函数的表达式；

②出该二次函数的大致图象，并借助函数图象，求不等式的解集；

当取，时，二次函数图象与轴正半轴分别交于点，点．如果点在点的右边，且点和点都在点的右边．试比较和的大小．

Answer 1

【答案】①；②；．

【解析】

（1）①已知抛物线图象上的两点坐标，且只有两个待定系数，利用待定系数法求解即可；
②画出函数图象，根据图形求出不等式ax2+bx+2≥0的解集；
（2）用a表示出函数的解析式，然后分别将M、N的坐标代入抛物线的解析式中，分别用m、n表示出a1、a2，通过做差可比较出a1、a2的大小．

①∵二次函数经过点和

可得，解得，

即二次函数的表达式为：；

②如图：由图象得：不等式的解集为：；

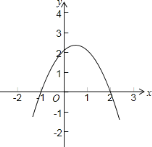
∵二次函数与轴正半轴交与点且

∴，

即，

同理，

故，

∵，

故，

∴．