题目内容
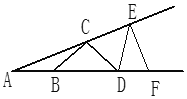
【题目】如图,∠EAF=15°,,AB=BC=CD=DE=EF,则∠EDF等于( )
A.90°B.75°C.70°D.60°
【答案】D
【解析】
在△ABC中可求得∠ACB,利用外角性质可求得∠CBD,则在△BCD中可求得∠BCD,利用邻补角可求得∠ECD,再利用外角的性质可得∠EDF=∠A+∠CED,可求得答案.
∵AB=BC,∠A=15°,
∴∠ACB=∠A=15°,∠CBD=2∠A=30°,
∵BC=DC,
∴∠CBD=∠CDB=30°,
∴∠BCD=120°,
∴∠ECD=180°∠ACB∠BCD=180°15°120°=45°,
∵CD=DE,
∴∠CED=∠DCE=45°,
∴∠EDF=∠A+∠CED=15°+45°=60°,
故选D.

练习册系列答案
相关题目