题目内容
【题目】已知![]() 是
是![]() 的反比例函数,并且当
的反比例函数,并且当![]() 时,
时,![]() .
.
![]() 求
求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
![]() 当
当![]() 时,
时,![]() 的值为________;该函数的图象位于第________象限,在图象的每一支上,
的值为________;该函数的图象位于第________象限,在图象的每一支上,![]() 随
随![]() 的增大而________.
的增大而________.
![]() 直接写出此反比例函数与直线
直接写出此反比例函数与直线![]() 的交点坐标.
的交点坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;一、三;减小.
;一、三;减小.![]() 和
和![]() .
.
【解析】
(1)根据点(2,8)利用待定系数法即可求出反比例函数解析式;
(2)将x=4代入反比例函数解析式中求出y值,再由k=16>0结合反比例函数图象即可得出结论;
(3)联立两函数解析式成方程组,通过解方程组即可求出两函数图象的交点坐标.
(1)设y关于x的函数解析式为y=![]() (k≠0),
(k≠0),
将(2,8)代入y=![]() ,
,
8=![]() ,解得:k=16,
,解得:k=16,
∴y关于x的函数解析式为y=![]() .
.
(2)当x=4时,y=![]() =4;
=4;
∵k=16>0,
∴反比例函数y=![]() 的图象位于第一、三象限,且在图象的每一支上,y随x的增大而减小.
的图象位于第一、三象限,且在图象的每一支上,y随x的增大而减小.
故答案为:4;一、三;减小.
3)联立两函数解析式成方程组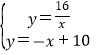 ,
,
解得:![]() ,
,![]() .
.
∴此反比例函数与直线y=x+10的交点坐标为(2,8)和(8,2).

练习册系列答案
相关题目