Question

【题目】如图，在⊙O中，AC是弦，AD是切线，CB⊥AD于B，CB与⊙O相交于点E，连接AE，若AE平分∠BAC，BE=1，则CE= ．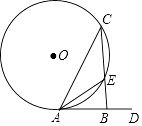

Answer 1

【答案】2
【解析】解：∵AD是切线，

∴∠C=∠BAE，

∵∠BAE=∠CAE，

∴∠C=∠BAE=∠CAE，

∵CB⊥AD，

∴∠C+∠BAE+∠CAE=90°，

∴∠C=∠BAE=∠CAE=30°，

∴CE=AE=2BE=2，

所以答案是2．

【考点精析】认真审题，首先需要了解角的平分线(从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线)，还要掌握含30度角的直角三角形(在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键．