题目内容
【题目】综合题
(1)如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DFDA=DBDC;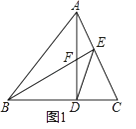
(2)如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DFDG,请画出图形找出点G并加以证明;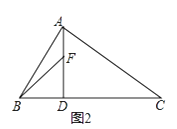
(3)如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.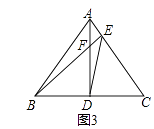
【答案】
(1)解:证明:如图1中,
∵AD、AE是△ABC的高,
∴∠ADC=∠BDF=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∴△DBF∽△DAC,
∴ ![]() =
= ![]() ,
,
∴DFDA=DBDC.
(2)解:如图2中,在DC上截取DM,使得DM=DA,
连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DFDG.
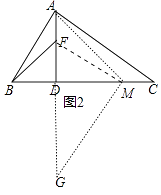
理由:∵∠MDF=∠MDG=∠FMG=90°,
∴∠DMF+∠DMG=90°,∠DMG+∠G=90°,
∴∠DMF=∠G,
∴△DMF∽△DGM,
∴ ![]() =
= ![]() ,
,
∴DM2=DFDG,
∵AD=DM,
∴AD2=DFDG.
(3)解:如图3中,连接FC.
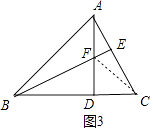
∵∠ABC=45°,∠ADB=90°,
∴BD=AD,
∵∠DBF=∠CAD(已证),∠BDF=∠ADC=90°,
∴△BDF≌△ADC,
∴DF=DC,
在Rt△EFC中,FC= ![]() =
= ![]() =
= ![]() ,
,
∴DF=DC= ![]() ,设BD=AD=y,则AC=
,设BD=AD=y,则AC= ![]() =
= ![]() ,
,
∵△EAF∽△DAC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得y=2 ![]() 或
或 ![]() (舍弃),
(舍弃),
∴BD=2 ![]() .
.
【解析】(1)先证明∠DBF=∠DAC,然后再证明△DBF∽△DAC,最后,依据相似三角形对应边成比例求解即可;
(2)在DC上截取DM,使得DM=DA,连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DFDG.接下来,再证明△DMF∽△DGM即可解决问题;
(3)连接FC.依据ASA可证明△BDF≌△ADC,根据全等三角形的性质定理可得到DF=DC,接下来,依据勾股定理可求得DF、DC的长,设BD=AD=y,则可得到AC的长,最后,依据△EAF∽△DAC,可得到关于y的比例式,从而可求得y的值.
【考点精析】掌握相似三角形的应用是解答本题的根本,需要知道测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案