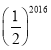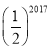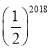题目内容
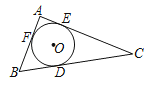
【题目】如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
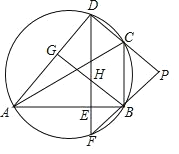
(1)求证:∠BAD=∠PCB;
(2)求证:BG//CD;
(3)设△ABC外接圆的圆心为O,连接OD,OH,若弦BC的长等于圆的半径,∠COD=20°,求∠OHD的度数.
【答案】(1)见解析;(2)见解析;(3)70
【解析】
(1)根据等腰三角形的性质和圆内接四边形的性质即可得到结论;
(2)由(1)得∠BAD=∠PCB,结合等腰三角形的性质及同弧所对的圆周角相等可得∠BFD=∠PBC,根据平行线的判定得:BC∥DF,可得∠ABC=90°,根据圆周角定理得到AC是⊙O的直径,可证∠ADC=∠AGB=90°,即可得证;
(3)连接OB,由(2)可得点O在AC的中点.由弦BC的长等于圆的半可得三角形OBC为等边三角形,∠OCB=60°,则∠BAC=30°,因为∠COD=20°,故可求得∠ODA=∠OAD=10°,则∠ADH=50°,求得∠ODH=40°,
由(2)可证四边形DHBC为平行四边形,所以DH=BC=OD,即可根据等腰三角形的性质和三角形的内角和定理求出∠OHD.
(1) ∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)连接OB,由(2)可得:点O在AC的中点.

∵弦BC的长等于圆的半径
∴△OBC为等边三角形
∴∠OCB=60°
由(2)得:∠ABC=90°,
∴∠BAC=30°
∵∠COD=20°
∴∠ODA=∠OAD=![]() ∠COD=10°
∠COD=10°
∴∠ADE=90°-30°-10°=50°
∴∠ODH=∠ADH-∠ADO=40°
由(2)得:DF∥BC,BG∥CD
∴四边形DHBC为平行四边形
∴DH=BC=OD
∴∠OHD=![]()

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案