题目内容
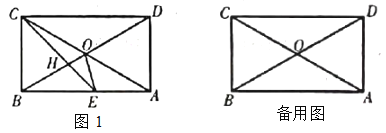
【题目】如图,矩形![]() 中,
中,![]() ,对角线
,对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 的平分线
的平分线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() .
.
(l)求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)求![]() .
.
【答案】(1)75°;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由矩形的性质可得AB∥CD,AO=CO=BO=DO,由角平分线的性质和平行线的性质可求BC=BE=BO,即可求解;
(2)过点H作FH⊥BC于F,由直角三角形的性质可得FH=![]() BF,BC=
BF,BC=![]() BF+BF=1,可求BH的长,由三角形面积公式可求△BCH的面积;
BF+BF=1,可求BH的长,由三角形面积公式可求△BCH的面积;
(3)过点C作CN⊥BO于N,由直角三角形的性质可求BC=![]() BF+BF=BO=BE,OH=OB-BH=
BF+BF=BO=BE,OH=OB-BH=![]() BF-BF,CN=
BF-BF,CN=![]() BC=
BC=![]() BF,即可求解.
BF,即可求解.
解:(1)∵四边形ABCD是矩形
∴AB∥CD,AO=CO=BO=DO,
∴∠DCE=∠BEC,
∵CE平分∠BCD
∴∠BCE=∠DCE=45°,
∴∠BCE=∠BEC=45°
∴BE=BC
∵∠BAC=30°,AO=BO=CO
∴∠BOC=60°,∠OBA=30°
∵∠BOC=60°,BO=CO
∴△BOC是等边三角形
∴BC=BO=BE,且∠OBA=30°
∴∠BOE=75°
(2)如图,过点H作FH⊥BC于F,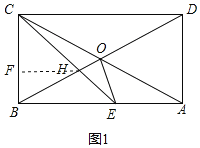
∵△BOC是等边三角形
∴∠FBH=60°,FH⊥BC
∴BH=2BF,FH=![]() BF,
BF,
∵∠BCE=45°,FH⊥BC
∴CF=FH=![]() BF
BF
∴BC=![]() BF+BF=1
BF+BF=1
∴BF=![]() ,
,
∴FH=![]() ,
,
∴S△BCH=![]() ×BC×FH=
×BC×FH=![]() ;
;
(3)如图,过点C作CN⊥BO于N,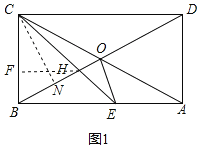
∵△BOC是等边三角形
∴∠FBH=60°,FH⊥BC
∴BH=2BF,FH=![]() BF,
BF,
∵∠BCE=45°,FH⊥BC
∴CF=FH=![]() BF
BF
∴BC=![]() BF+BF=BO=BE,
BF+BF=BO=BE,
∴OH=OB-BH=![]() BF-BF
BF-BF
∵∠CBN=60°,CN⊥BO
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某学校准备为七年级学生开设![]() 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课 |
|
|
|
|
|
|
人数 | 40 | 60 | 100 |
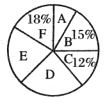
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.![]() 对应扇形的圆心角为
对应扇形的圆心角为![]()
C.喜欢选修课![]() 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课![]() 的人数最少
的人数最少