ЬтФПФкШн
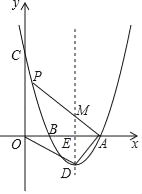
ЁОЬтФПЁПШчЭМЃЌжБЯпy=Љ![]() x+cгыxжсНЛгкЕуAЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЌХзЮяЯпy=Љ
x+cгыxжсНЛгкЕуAЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЌХзЮяЯпy=Љ![]() x2+bx+cОЙ§ЕуAЃЌBЃЎ
x2+bx+cОЙ§ЕуAЃЌBЃЎ
ЃЈ1ЃЉЧѓЕуBЕФзјБъКЭХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉMЃЈmЃЌ0ЃЉЮЊxжсЩЯвЛЖЏЕуЃЌЙ§ЕуMЧвДЙжБгкxжсЕФжБЯпгыжБЯпABМАХзЮяЯпЗжБ№НЛгкЕуPЃЌNЃЎ
ЂйЕуMдкЯпЖЮOAЩЯдЫЖЏЃЌШєвдBЃЌPЃЌNЮЊЖЅЕуЕФШ§НЧаЮгыЁїAPMЯрЫЦЃЌЧѓЕуMЕФзјБъЃЛ
ЂкЕуMдкxжсЩЯздгЩдЫЖЏЃЌШєШ§ИіЕуMЃЌPЃЌNжаЧЁгавЛЕуЪЧЦфЫќСНЕуЫљСЌЯпЖЮЕФжаЕуЃЈШ§ЕужиКЯГ§ЭтЃЉЃЌдђГЦMЃЌPЃЌNШ§ЕуЮЊЁАЙВаГЕуЁБЃЎЧыжБНгаДГіЪЙЕУMЃЌPЃЌNШ§ЕуГЩЮЊЁАЙВаГЕуЁБЕФmЕФжЕЃЎ

ЁОД№АИЁП(1)ХзЮяЯпНтЮіЪНЮЊy=Љ![]() x2+
x2+![]() x+2ЃЛ(2)ЂйЕуMЕФзјБъЮЊЃЈ2.5ЃЌ0ЃЉЛђЃЈ
x+2ЃЛ(2)ЂйЕуMЕФзјБъЮЊЃЈ2.5ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЛЂкmЕФжЕЮЊ
ЃЌ0ЃЉЃЛЂкmЕФжЕЮЊ![]() ЛђЉ1ЛђЉ
ЛђЉ1ЛђЉ![]() ЃЎ
ЃЎ
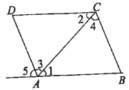
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбAЕузјБъДњШыжБЯпНтЮіЪНПЩЧѓЕУcЃЌдђПЩЧѓЕУBЕузјБъЃЌгЩAЁЂBЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЂйгЩMЕузјБъПЩБэЪОPЁЂNЕФзјБъЃЌДгЖјПЩБэЪОГіMAЁЂMPЁЂPNЁЂPBЕФГЄЃЌЗжЁЯNBP=90ЁуКЭЁЯBNP=90ЁуСНжжЧщПіЃЌЗжБ№РћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЕНЙигкmЕФЗНГЬЃЌПЩЧѓЕУmЕФжЕЃЛ
ЂкгУmПЩБэЪОГіMЁЂPЁЂNЕФзјБъЃЌгЩЬтвтПЩжЊгаPЮЊЯпЖЮMNЕФжаЕуЁЂMЮЊЯпЖЮPNЕФжаЕуЛђNЮЊЯпЖЮPMЕФжаЕуЃЌПЩЗжБ№ЕУЕНЙигкmЕФЗНГЬЃЌПЩЧѓЕУmЕФжЕЃЎ
ЪдЬтНтЮіЃКНтЃК
ЃЈ1ЃЉЁп![]() гыxжсНЛгкЕуAЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЌЁр0=Љ2+cЃЌНтЕУc=2ЃЌЁрBЃЈ0ЃЌ2ЃЉЃЌЁпХзЮяЯп
гыxжсНЛгкЕуAЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЌЁр0=Љ2+cЃЌНтЕУc=2ЃЌЁрBЃЈ0ЃЌ2ЃЉЃЌЁпХзЮяЯп![]() ОЙ§ЕуAЃЌBЃЌЁр
ОЙ§ЕуAЃЌBЃЌЁр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК 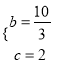 ЃЌЁрХзЮяЯпНтЮіЪНЮЊ
ЃЌЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйгЩЃЈ1ЃЉПЩжЊжБЯпНтЮіЪНЮЊ![]() ЃЌЁпMЃЈmЃЌ0ЃЉЮЊxжсЩЯвЛЖЏЕуЃЌЙ§ЕуMЧвДЙжБгкxжсЕФжБЯпгыжБЯпABМАХзЮяЯпЗжБ№НЛгкЕуPЃЌNЃЌЁрPЃЈmЃЌ
ЃЌЁпMЃЈmЃЌ0ЃЉЮЊxжсЩЯвЛЖЏЕуЃЌЙ§ЕуMЧвДЙжБгкxжсЕФжБЯпгыжБЯпABМАХзЮяЯпЗжБ№НЛгкЕуPЃЌNЃЌЁрPЃЈmЃЌ ![]() ЃЉЃЌNЃЈmЃЌ
ЃЉЃЌNЃЈmЃЌ ![]() ЃЉЃЌЁрPM=
ЃЉЃЌЁрPM=![]() ЃЌPA=3ЉmЃЌPN=
ЃЌPA=3ЉmЃЌPN=![]() ЉЃЈ
ЉЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌЁпЁїBPNКЭЁїAPMЯрЫЦЃЌЧвЁЯBPN=ЁЯAPMЃЌЁрЁЯBNP=ЁЯAMP=90ЁуЛђЁЯNBP=ЁЯAMP=90ЁуЃЌЗжСНжжЧщПіЃК
ЃЌЁпЁїBPNКЭЁїAPMЯрЫЦЃЌЧвЁЯBPN=ЁЯAPMЃЌЁрЁЯBNP=ЁЯAMP=90ЁуЛђЁЯNBP=ЁЯAMP=90ЁуЃЌЗжСНжжЧщПіЃК
ЕБЁЯBNP=90ЁуЪБЃЌдђгаBNЁЭMNЃЌЁрЕуNЕФзнзјБъЮЊ2ЃЌЁр ![]() =2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=
=2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=![]() ЃЌЁрMЃЈ
ЃЌЁрMЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЕБЁЯNBP=90ЁуЪБЃЌдђга![]() ЃЌЁпAЃЈ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ2ЃЉЃЌPЃЈmЃЌ
ЃЌЁпAЃЈ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ2ЃЉЃЌPЃЈmЃЌ ![]() ЃЉЃЌЁрBP=
ЃЉЃЌЁрBP=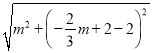 =
= ![]() ЃЌAP=
ЃЌAP=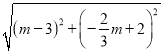 =
=![]() ЃЈ3ЉmЃЉЃЌЁр
ЃЈ3ЉmЃЉЃЌЁр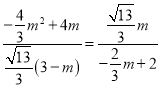 ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=
ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=![]() ЃЌЁрMЃЈ
ЃЌЁрMЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
злЩЯПЩжЊЕБвдBЃЌPЃЌNЮЊЖЅЕуЕФШ§НЧаЮгыЁїAPMЯрЫЦЪБЃЌЕуMЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂкгЩЂйПЩжЊMЃЈmЃЌ0ЃЉЃЌPЃЈmЃЌ ![]() ЃЉЃЌNЃЈmЃЌ
ЃЉЃЌNЃЈmЃЌ ![]() ЃЉЃЌЁпMЃЌPЃЌNШ§ЕуЮЊЁАЙВаГЕуЁБЃЌЁргаPЮЊЯпЖЮMNЕФжаЕуЁЂMЮЊЯпЖЮPNЕФжаЕуЛђNЮЊЯпЖЮPMЕФжаЕуЃЌЕБPЮЊЯпЖЮMNЕФжаЕуЪБЃЌдђга2ЃЈ
ЃЉЃЌЁпMЃЌPЃЌNШ§ЕуЮЊЁАЙВаГЕуЁБЃЌЁргаPЮЊЯпЖЮMNЕФжаЕуЁЂMЮЊЯпЖЮPNЕФжаЕуЛђNЮЊЯпЖЮPMЕФжаЕуЃЌЕБPЮЊЯпЖЮMNЕФжаЕуЪБЃЌдђга2ЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌНтЕУm=3ЃЈШ§ЕужиКЯЃЌЩсШЅЃЉЛђm=
ЃЌНтЕУm=3ЃЈШ§ЕужиКЯЃЌЩсШЅЃЉЛђm=![]() ЃЛ
ЃЛ
ЕБMЮЊЯпЖЮPNЕФжаЕуЪБЃЌдђга![]() +ЃЈ
+ЃЈ![]() ЃЉ=0ЃЌНтЕУm=3ЃЈЩсШЅЃЉЛђm=Љ1ЃЛ
ЃЉ=0ЃЌНтЕУm=3ЃЈЩсШЅЃЉЛђm=Љ1ЃЛ
ЕБNЮЊЯпЖЮPMЕФжаЕуЪБЃЌдђга![]() =2ЃЈ
=2ЃЈ![]() ЃЉЃЌНтЕУm=3ЃЈЩсШЅЃЉЛђm=
ЃЉЃЌНтЕУm=3ЃЈЩсШЅЃЉЛђm=![]() ЃЛ
ЃЛ
злЩЯПЩжЊЕБMЃЌPЃЌNШ§ЕуГЩЮЊЁАЙВаГЕуЁБЪБmЕФжЕЮЊ![]() ЛђЉ1Лђ
ЛђЉ1Лђ![]() ЃЎ
ЃЎ

 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИЁОЬтФПЁПШчЭМЃЌгЩгкИїШЫЕФЯАЙпВЛЭЌЃЌЫЋЪжНЛВцЪБзѓЪжДѓФДжИЛђгвЪжДѓФДжИдкЩЯЪЧвЛИіЫцЛњЪТМўЃЌдјРЯЪІЖдЫћШЮНЬЕФбЇЩњзіСЫвЛИіЕїВщЃЌЭГМЦНсЙћШчЯТБэЫљЪОЃК
2011Нь | 2012Нь | 2013Нь | 2014Нь | 2015Нь | |
ВЮгыЪЕбщЕФШЫЪ§ | 106 | 110 | 98 | 104 | 112 |
гвЪжДѓФДжИдкЩЯЕФШЫЪ§ | 54 | 57 | 49 | 51 | 56 |
ЦЕТЪ | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
ИљОнБэИёжаЕФЪ§ОнЃЌФуШЯЮЊдкетИіЫцЛњЪТМўжаЃЌгвЪжДѓФДжИдкЩЯЕФИХТЪПЩвдЙРМЦЮЊЃЈЁЁЁЁЃЉ

A. 0.6 B. 0.5 C. 0.45 D. 0.4