题目内容
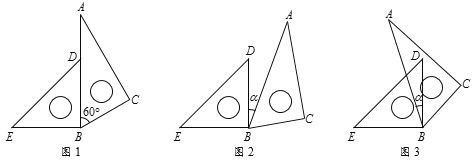
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )

A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
【答案】C
【解析】分析:根据已知条件易证△CFG≌△EDG,可得FG=EG,CG=DG,根据对角线互相平分的四边形为平行四边形即可判定四边形CEDF是平行四边形;再由CE⊥AD,根据有一个角为直角的平行四边形为矩形即可判定平行四边形CEDF是矩形;再证明△CED为等边三角形,可得CE=DE,根据一组邻边相等的平行四边形为菱形即可得平行四边形CEDF是菱形;采用排除法即可得答案.
详解:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
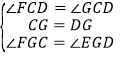 ,
,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
∵CE⊥AD,
∴平行四边形CEDF是矩形;
∵四边形ABCD是平行四边形,
∴∠B=∠ADC=60°;
∵∠AEC=120°,
∴∠DEC=60°;
∴∠DEC=∠ADC=60°,
∴△CED为等边三角形,
∴CE=DE,
∴平行四边形CEDF是菱形;
综上,选项A、B、D正确,选项D错误,故选C.

【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段 | 销售数量 | 销售收入 (元) | |
A种型号 (台) | B种型号 (台) | ||
第一周 | 3 | 2 | 3960 |
第二周 | 5 | 4 | 7120 |
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?