题目内容
【题目】![]() 中,
中,![]() .设
.设![]() 的面积为
的面积为![]() .
.

①图1中,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的四点;
上的四点;
②图2中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 交于点
交于点![]() ;
;
③图3中,![]() ,D为
,D为![]() 中点,
中点,![]() .
.
其中,阴影部分面积为![]() 的是______(填序号).
的是______(填序号).
【答案】①②③.
【解析】
由等腰三角形的性质可判断①,由等边三角形的性质可判断②,由ASA可证△ADF≌△DBE,可得S△ADF=S△DBE,即可判断③.
如图1,∵AB=AC,点D是BC中点,
∴BD=CD,AD垂直平分BC,
∴S△BDN=S△DCN,S△BMN=S△MNC,S△BFM=S△CFM,S△EFB=S△EFC,S△AEB=S△AEC,
∴阴影部分面积为![]() S;
S;
如图2,∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,且AD⊥BC,BE⊥AC,CF⊥AB,
∴AD垂直平分BC,BE垂直平分AC,CF垂直平分AB,
∴S△BDO=S△CDO,S△AEO=S△CEO,S△AFO=S△BFO,
∴阴影部分面积为![]() S;
S;
如图3,连接AD,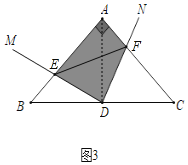
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD=BD,∠B=∠DAC=45°,AD⊥BC,
∴∠ADM+∠BDM=90°,且∠MDA+∠ADN=90°,
∴∠BDM=∠ADN,且AD=BD,∠B=∠DAC=45°,
∴△ADF≌△DBE(ASA)
∴S△ADF=S△DBE,
∴阴影部分面积为![]() S;
S;
故答案为:①②③.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目





