题目内容
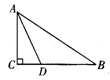
在△ABC中,AB=AC=12 cm,BC=6 cm,D为BC的中点,动点P从点B出发,以每秒1 cm的速度沿B→A→C的方向运动.设运动时间为t,那么当t=_______秒时,过D、P两点的直线将的△ABC周长分成两个部分,使其中一部分是另一部分的2倍.
7或17.
试题分析:由于动点P从B点出发,沿B→A→C的方向运动,所以分两种情况进行讨论:(1)P点在AB上,设运动时间为t,用含t的代数式分别表示BP,AP,根据条件过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍,求出t值;(2)P点在AC上,同理,可解出t的值:
分两种情况:
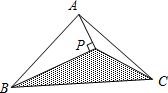
(1)P点在AB上时,如图,AB=AC=12cm,BD=CD=
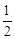 BC=
BC=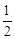 ×6=3cm,
×6=3cm,设P点运动了t秒,则BP=t,
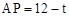 ,
,由题意得:BP+BD=
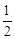 (AP+AC+CD),
(AP+AC+CD),∴
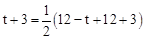 ,解得t=7秒.
,解得t=7秒.
(2)P点在AC上时,如图,AB=AC=12cm,BD=CD=
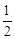 BC=
BC= ×6=3cm,
×6=3cm,P点运动了t秒,则AB+AP=t,
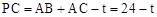 ,
,由题意得:BD+AB+AP=2(PC+CD),
∴
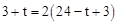 ,解得t=17秒.
,解得t=17秒.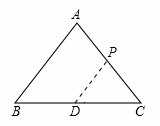
∴当t=7或17秒时,过D、P两点的直线将△ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
考点: 1.等腰三角形的性质;2.单动点问题;3.分类思想的应用.

练习册系列答案
相关题目

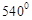 ,则这个多边形是【 】
,则这个多边形是【 】