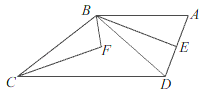
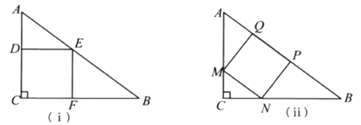
题目内容
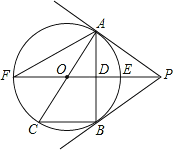
【题目】在矩形ABCD中,AB=12,BC=25,P是线段AB上一点(点P不与A,B重合),将△PBC沿直线PC折叠,顶点B的对应点是点G,CG,PG分别交线段AD于E,O.
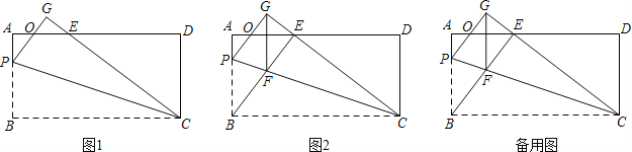
(1)如图1,若OP=OE,求证:AE=PB;
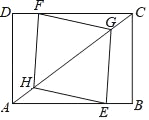
(2)如图2,连接BE交PC于点F,若BE⊥CG.
①求证:四边形BFGP是菱形;
②当AE=9,求![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)由折叠的性质可得PB=PG,∠B=∠G=90°,由“AAS”可证△AOP≌△GOE,可得OA=GO,即可得结论;
(2)①由折叠的性质可得∠PGC=∠PBC=90°,∠BPC=∠GPC,BP=PG,BF=FG,由平行线的性质可得∠BPF=∠BFP=∠GPC,可得BP=BF,即可得结论;
②由勾股定理可求BE的长,EC的长,由相似三角形的性质可得![]() ,可求BF=BP=5x=
,可求BF=BP=5x=![]() ,由勾股定理可求PC的长,即可求解.
,由勾股定理可求PC的长,即可求解.
证明:(1)∵四边形ABCD是矩形
∴AB=CD,AD=BC,AD∥BC,∠A=∠B=90°
∵将△PBC沿直线PC折叠,
∴PB=PG,∠B=∠G=90°
∵∠AOP=∠GOE,OP=OE,∠A=∠G=90°
∴△AOP≌△GOE(AAS)
∴AO=GO
∴AO+OE=GO+OP
∴AE=GP,
∴AE=PB,
(2)①∵△BPC沿PC折叠得到△GPC,
∴∠PGC=∠PBC=90°,∠BPC=∠GPC,BP=PG,BF=FG
∵BE⊥CG,
∴BE∥PG,
∴∠GPF=∠PFB,
∴∠BPF=∠BFP,
∴BP=BF
∴BP=BF=PG=GF
∴四边形BFGP是菱形;
②∵AE=9,CD=AB=12,AD=BC=GC=25,
∴DE=AD-AE=16,BE=![]() =15,
=15,
在Rt△DEC中,EC=![]() =20
=20
∵BE∥PG
∴△CEF∽△CGP
∴![]()
∴![]() =
=![]() =
=![]()
∴设EF=4x,PG=5x,
∴BF=BP=GF=5x,
∵BF+EF=BE=15
∴9x=15
∴x=![]()
∴BF=BP=5x=![]() ,
,
在Rt△BPC中,PC=![]() =
=![]()
∴![]() =
=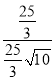 =
=![]()