题目内容
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() ,连接
,连接![]() 并延长,分别交
并延长,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
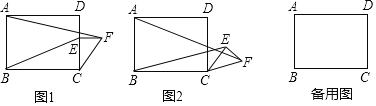
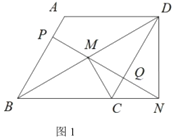
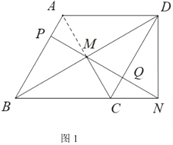
(1)如图1,若![]() 且
且![]() ,求菱形
,求菱形![]() 的面积;
的面积;
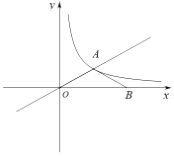
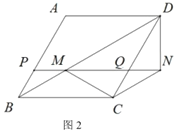
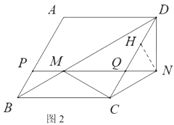
(2)如图2,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)连接![]() ,可得
,可得![]() ,进而得
,进而得![]() 、
、![]() 、
、![]() 三点共线,点M是菱形
三点共线,点M是菱形![]() 的旋转中心,可得
的旋转中心,可得![]() ,结合旋转的性质可得
,结合旋转的性质可得![]() ,MQ=NQ,根据直角三角形的性质得
,MQ=NQ,根据直角三角形的性质得![]() ,BM=4
,BM=4![]() ,进而即可求解;
,进而即可求解;
(2)根据菱形的性质和旋转的性质以及SAS,可证![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,可证
,可证![]() ,再证
,再证![]() ,即可得到结论.
,即可得到结论.
(1)连接![]() ,如图1,
,如图1,
∵在菱形![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() 、
、![]() 、
、![]() 三点共线,点M是菱形
三点共线,点M是菱形![]() 的旋转中心,
的旋转中心,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵CM=CN,
∴![]() ,MQ=NQ,
,MQ=NQ,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠MBC=![]() ∠ABC=30°,
∠ABC=30°,
∴BM=4![]() ,
,
∴![]() 菱形
菱形![]() =32
=32![]() ;
;
(2)四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
由旋转的性质得:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵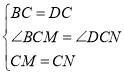 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 上取点
上取点![]() ,使
,使![]() ,如图2,
,如图2,
在![]() 和
和![]() 中,
中,
∵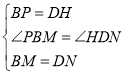 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴∠DHN=∠CQN,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下: (说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下)
收集数据
10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据
整理、描述样本数据,绘制统计表如下:
抽取的30名学生物理实验操作考核成绩频数统计表
成绩等级 | A | B | C | D |
人数(名) | 10 | m | n | 3 |
根据表中的信息,解答下列问题:
(1)m=________,n=________;
(2)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
(3)甲、乙、丙、丁是九年级1班物理实验考核成绩为10分的四名学生,学校计划从这四名学生中随机选出两名学生代表学校去参加全市中学生“物理实验操作”竞赛,用列表法或画树状图法,求甲、乙两名学生中至少有一名被选中的概率.