题目内容
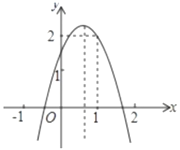
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 且与
且与![]() 轴交点的横坐标分别为
轴交点的横坐标分别为![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中结论正确的有( ).
,其中结论正确的有( ).
A.1个B.2个C.3个D.4个
【答案】D
【解析】
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴的位置,判断b的符号,即可判断①;根据x=2所对应的函数值,即可判断②;根据![]() <1,b>0,即可判断③;根据顶点的纵坐标>2,即可判断④;根据抛物线过点(1,2),x=1,x=2所对应的函数值<0,即可判断⑤.
<1,b>0,即可判断③;根据顶点的纵坐标>2,即可判断④;根据抛物线过点(1,2),x=1,x=2所对应的函数值<0,即可判断⑤.
由抛物线的开口向下知:a<0,与y轴的交点为在y轴的正半轴上,得:c>0,
∵对称轴为:直线x=![]() >0,
>0,
∴b>0,
∴![]() ,故①错误;
,故①错误;
∵当x=2时,y=4a+2b+c<0,
∴②正确;
∵![]() <1,a<0,
<1,a<0,
∴2a+b<0,
∵b>0,
∴-2b<0,
∴2a-b=2a+b+(-2b)<0,
∴③正确;
∵![]() >2,
>2,
∴4acb2<8a,
∴b2+8a>4ac,
∴④正确;
∵二次函数![]() 的图象经过点
的图象经过点![]() ,
,
∴a+b+c=2,则2a+2b+2c=4(i),
∵当x=2时,y=4a+2b+c<0(ii),
当x=1时,y=ab+c<0,则2a2b+2c<0(iii),
由(i)(iii)得:2a+2c<2,
由(i)(ii)得:2ac<4,即:4a2c<8,
上面两个不等式相加得到:6a<6,
∴a<1,故⑤正确;
∴②③④⑤正确.
故选D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下: (说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下)
收集数据
10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据
整理、描述样本数据,绘制统计表如下:
抽取的30名学生物理实验操作考核成绩频数统计表
成绩等级 | A | B | C | D |
人数(名) | 10 | m | n | 3 |
根据表中的信息,解答下列问题:
(1)m=________,n=________;
(2)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
(3)甲、乙、丙、丁是九年级1班物理实验考核成绩为10分的四名学生,学校计划从这四名学生中随机选出两名学生代表学校去参加全市中学生“物理实验操作”竞赛,用列表法或画树状图法,求甲、乙两名学生中至少有一名被选中的概率.
【题目】某公司购进一批新产品进行销售,已知该产品的进货单价为8元/件,该公司对这批新产品上市后的销售情况进行了跟踪调查.销售过程中发现,该产品每月的销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系满足下表.
(元)之间的关系满足下表.
销售单价 | … | 10 | 12 | 14 | 15 | … |
每月销售量 | … | 40 | 36 | 32 | 30 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当销售单价为多少元时,该产品每月获得的利润为240万元?
(3)如果该产品每月的进货成本不超过160万元,那么当销售单价为多少元时,该产品每月获得的利润最大?最大利润为多少万元?