题目内容
【题目】小亮和爸爸登山,两人距地面的高度![]() (米)与小亮登山时间
(米)与小亮登山时间![]() (分)之间的函数图象分别如图中折线
(分)之间的函数图象分别如图中折线![]() 和线段
和线段![]() 所示,根据函数图形进行一下探究:
所示,根据函数图形进行一下探究:

(1)设线段![]() 所表示的函数关系式为
所表示的函数关系式为![]() ,根据图象求
,根据图象求![]() 的值,并写出
的值,并写出![]() 的实际意义;
的实际意义;
(2)若小亮提速后,他登山的速度是爸爸速度的3倍,问:小亮登山多长时间时开始提速?此时小亮距地面的高度是多少米?
【答案】(1)![]() ;
;![]()
![]() 表示小亮爸爸的平均登山速度;
表示小亮爸爸的平均登山速度;
![]() 表示小亮爸爸从距地面100米开始登山;
表示小亮爸爸从距地面100米开始登山;
(2)小亮登山2分钟时开始提速,此时小亮距地面的高度为30米.
【解析】
(1)根据图像可知(0,100);(20,300)在线段DE所表示的函数上,从而可解答本题.
(2)分别求出OA段和AC段所对应的函数解析式联立方程组,可求得A点的坐标,从而解答本题.
(1)由图像可知:(0,100);(20,300)在线段DE所表示的函数![]() 上
上
∴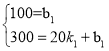 解得
解得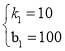
![]() 表示小亮爸爸的平均登山速度;
表示小亮爸爸的平均登山速度;
![]() 表示小亮爸爸从距地面100米开始登山;
表示小亮爸爸从距地面100米开始登山;
(2)由图像可知,点(1,15)在OA段所在的函数图像上,设OA段函数解析式为![]()
∴解得![]() OA段函数解析式为
OA段函数解析式为![]()
点B(m,165)在![]() 上,解得
上,解得![]() ,即点B的坐标为(6.5,165)
,即点B的坐标为(6.5,165)
∵小亮提速后,他登山的速度是爸爸速度的3倍,小亮爸爸的速度为10米/分,点B在AC段上,设AC段的解析式为![]() 可得
可得![]()
∴AC段的函数解析式为![]()
∵点A为OA,AC段的交点
∴![]() 解得
解得![]() 即点A的坐标为(2,30)
即点A的坐标为(2,30)
即小亮登山2分钟时开始提速,此时小亮距地面的高度为30米.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目