题目内容
【题目】如图,锐角△ABC中,边BC长为3,高AH长为2,矩形EFMN的边MN在BC边上,其余两个顶点E,F分别在AB,AC边上,EF交AH于点G.
(1)求![]() 的值;
的值;
(2)当EN为何值时,矩形EFMN的面积为△ABC面积的四分之一.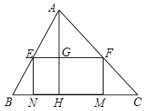
【答案】解:(1)∵EF∥BC,
∴△AEF∽△ABC,
∴![]() ,
,
∴![]() =
=![]() ;
;
(2)设EN=x,
∵EF∥BC,
∴△AEF∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴EF=3﹣![]() x,
x,
∵矩形EFMN的面积为△ABC面积的四分之一,
∴x(3﹣![]() x)=
x)=![]() ×
×![]() ×3×2,
×3×2,
∴x=1﹣![]() ,x=1+
,x=1+![]() ,
,
∴EN为1﹣![]() 或1+
或1+![]() 时,矩形EFMN的面积为△ABC面积的四分之一.
时,矩形EFMN的面积为△ABC面积的四分之一.
【解析】(1)由EF∥BC,得到△AEF∽△ABC,根据相似三角形的性质得到![]() , 根据比例的性质即可得到结论;
, 根据比例的性质即可得到结论;
(2)设EN=x,根据相似三角形的性质得到![]() , 代入数据得到
, 代入数据得到![]() , 求得EF=3﹣
, 求得EF=3﹣![]() x,根据题意列方程即可得到结论.
x,根据题意列方程即可得到结论.
【考点精析】掌握矩形的性质和相似三角形的判定与性质是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目