题目内容
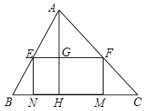
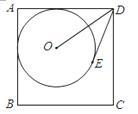
【题目】如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE交DO的延长线于点E,F是DE与⊙O的交点,连接BD,BF.
(1)求证:∠CDE=∠E;
(2)若OD=4,EF=1,求CD的长.
【答案】证明:(1)∵在⊙O中,直径AB交弦CD于点G,CG=DG,
∴AB⊥CD,
∵BE是⊙O的切线,
∴AB⊥BE,
∴CD∥BE,
∴∠CDE=∠E;
(2)解:∵∠CDE=∠E,∠DOG=∠BOE,
∴△ODG∽△OEB,
∴![]() ,
,
∵OD=4,EF=1,
∴OB=OF=OD=4,
∴OE=OF+EF=5,
∴![]() ,
,
∴OG=![]() ,
,
∴DG=![]() =
=![]() ,
,
∴CD=2DG=![]() .
.
【解析】(1)由在⊙O中,直径AB交弦CD于点G,CG=DG,根据垂径定理即可得AB⊥CD,又由BE是⊙O的切线,易证得CD∥BE,即可证得结论;
(2)易证得△ODG∽△OEB,然后由相似三角形的对应边成比例,求得OG的长,由勾股定理即可求得DG的长,继而求得答案.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
【题目】如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.5厘米,每个铁环长4.6厘米,设铁环间处于最大限度的拉伸状态
(1)填表:
铁环个数 | 1 | 2 | 3 | 4 |
链条长(cm) | 4.6 | 8.2 | _____ | ____ |
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成2.17米长的链条,至少需要多少个铁环?
![]()