题目内容
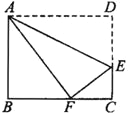
【题目】如图,AD为∠CAF的角平分线,BD=CD,∠DBC=∠DCB,∠DCA=∠ABD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】
根据角平分线上的点到角的两边距离相等可得DE=DF,再利用“HL”证明Rt△CDE和Rt△BDF全等,根据全等三角形对应边相等可得CE=AF,利用“HL”证明Rt△ADE和Rt△ADF全等,根据全等三角形对应边相等可得AE=AF,然后求出CE=AB+AE;根据全等三角形对应角相等可得∠DBF=∠DCE,然后求出A、B、C、D四点共圆,根据同弧所对的圆周角相等可得∠BDC=∠BAC;∠DAE=∠CBD,再根据全等三角形对应角相等可得∠DAE=∠DAF,然后求出∠DAF=∠CBD.
解:∵AD平分∠CAF,DE⊥AC,DF⊥AB,
∴DE=DF,
在Rt△CDE和Rt△BDF中,
![]()
∴Rt△CDE≌Rt△BDF(HL),故①正确;
∴CE=AF,
在Rt△ADE和Rt△ADF中,
![]() ,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∴CE=AB+AF=AB+AE,故②正确;
∵Rt△CDE≌Rt△BDF,
∴∠DBF=∠DCE
∴A、B、C、D四点共圆,
∴∠BDC=∠BAC,故③正确;
∠DAE=∠CBD,
∵Rt△ADE≌Rt△ADF,
∴∠DAE=∠DAF,
∴∠DAF=∠CBD,故④正确;
综上所述,正确的结论有①②③④共4个.
故选:A.

【题目】如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.5厘米,每个铁环长4.6厘米,设铁环间处于最大限度的拉伸状态
(1)填表:
铁环个数 | 1 | 2 | 3 | 4 |
链条长(cm) | 4.6 | 8.2 | _____ | ____ |
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成2.17米长的链条,至少需要多少个铁环?
![]()