题目内容
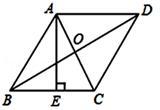
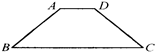
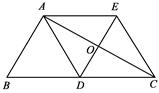
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
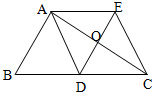
(1)求证:AD=EC;
(2)当∠BAC=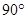 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形.

(1)求证:AD=EC;
(2)当∠BAC=
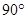 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形.通过平行四边形求证;菱形的判定
试题分析:(1)证明:∵DE∥AB,AE∥BC,
∴四边形ABDE是平行四边形,
∴AE∥BD,且AE=BD 2分
又∵AD是BC边上的中线,
∴BD=CD 4分
∴AE∥CD,且AE=CD
∴四边形ADCE是平行四边形,
∴AD="CE." 6分
(2)证明:∵∠BAC=
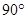 ,AD是斜边BC上的中线,
,AD是斜边BC上的中线,∴AD=BD=CD, 8分
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形
点评:本题属于对菱形的基本性质的运用和菱形的判定

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
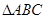 中,
中,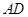 是边
是边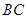 上的中线,过点
上的中线,过点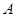 作
作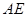 ∥
∥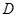 作
作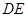 ∥
∥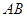 ,
,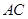 、
、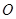 、点
、点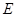 ,连接
,连接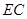 .
.
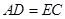 ;
;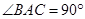 时,求证:四边形
时,求证:四边形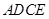 是菱形.
是菱形.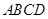 的面积为4,
的面积为4,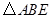 是等边三角形,点
是等边三角形,点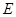 在正方形
在正方形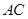 上有一点
上有一点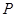 ,使
,使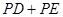 的和最小,则这个最小值为__________,
的和最小,则这个最小值为__________,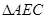 的面积为 __________
的面积为 __________ 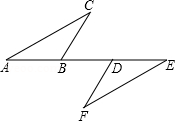
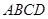 的对角线
的对角线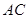 、
、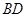 的长分别为
的长分别为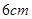 、
、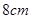 ,
,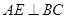 于点
于点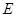 ,则
,则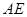 的长是
的长是 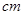 .
.