题目内容
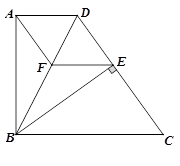
已知,矩形ABCD中,延长BC至E,使BE = BD,F为DE的中点,连结AF、CF.
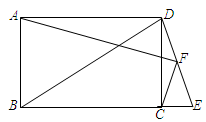
(1)若AB = 3,AD = 4,求CF的长;
(2)求证:∠ADB = 2∠DAF.

(1)若AB = 3,AD = 4,求CF的长;
(2)求证:∠ADB = 2∠DAF.
(1)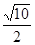 ;(2)连接BF,由BE=BD,EF=DF可证得∠DBF=∠EBF,再由CF=
;(2)连接BF,由BE=BD,EF=DF可证得∠DBF=∠EBF,再由CF=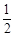 DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.
DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.
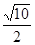 ;(2)连接BF,由BE=BD,EF=DF可证得∠DBF=∠EBF,再由CF=
;(2)连接BF,由BE=BD,EF=DF可证得∠DBF=∠EBF,再由CF=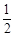 DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.
DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.试题分析:(1)根据矩形的性质可得
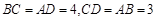 ,再根据个定理即可求的BD的长,从而可以求得BE、CE的长,再根据勾股定理即可求得DE的长,最后由F为DE的中点即可求得结果;
,再根据个定理即可求的BD的长,从而可以求得BE、CE的长,再根据勾股定理即可求得DE的长,最后由F为DE的中点即可求得结果;(2)连接BF,由BE=BD,EF=DF可证得∠DBF=∠EBF,再由CF=
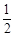 DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.
DE=DF即可证得∠DCF=∠FDC,从而可得∠ADF=BCF,再结合AD=BC即可证得△ADF≌△BCF,再根据全等三角形的性质即可作出判断.(1)∵因为四边形ABCD是矩形
∴
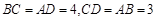
在RT△ABD中,
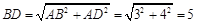
∴
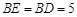 ,
,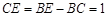
∴
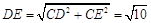
∵F是DE的中点
∴
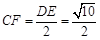 ;
;(2)连接BF
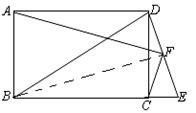
∵BE=BD,EF=DF
∴∠DBF=∠EBF
又∵CF=
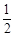 DE=DF
DE=DF∴∠DCF=∠FDC
∠ADC+∠CDF=∠BCD+∠DCF
即∠ADF=BCF
又∵AD=BC
∴△ADF≌△BCF
∴∠DAF=∠FBC=
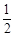 ∠DBE
∠DBE∵AD∥BC
∴∠ADB=∠DBE
∴∠ADB=2∠DAF.
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
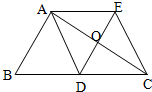
 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形.