题目内容
如图所示,正方形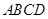 的面积为4,
的面积为4,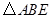 是等边三角形,点
是等边三角形,点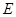 在正方形
在正方形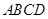 内,在对角线
内,在对角线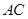 上有一点
上有一点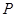 ,使
,使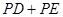 的和最小,则这个最小值为__________,
的和最小,则这个最小值为__________,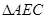 的面积为 __________
的面积为 __________ 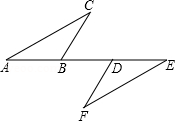
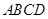 的面积为4,
的面积为4,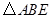 是等边三角形,点
是等边三角形,点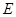 在正方形
在正方形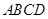 内,在对角线
内,在对角线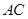 上有一点
上有一点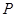 ,使
,使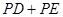 的和最小,则这个最小值为__________,
的和最小,则这个最小值为__________,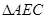 的面积为 __________
的面积为 __________ 
2,

试题分析:如图所示,正方形
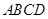 的面积为4,则AB=2;因为
的面积为4,则AB=2;因为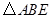 是等边三角形,所以AB=AE=BE=2;点
是等边三角形,所以AB=AE=BE=2;点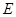 在正方形
在正方形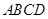 内,在对角线
内,在对角线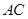 上有一点
上有一点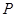 ,使
,使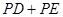 的和最小,根据图形,可得当P点在AC的中点,即P点是正方形
的和最小,根据图形,可得当P点在AC的中点,即P点是正方形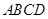 的中心时
的中心时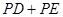 的和最小,这个最小值为=AB=2;因为正方形
的和最小,这个最小值为=AB=2;因为正方形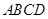 的边长为2,所以其对角线AC=
的边长为2,所以其对角线AC= ,
,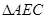 过E的高可求为
过E的高可求为 ,所以
,所以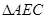 的面积为=
的面积为=

点评:本题考查正方形,解答本题需要掌握正方形的性质,熟悉等边三角形的性质,本题难度较大

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
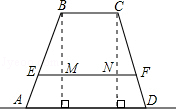
 的平分线
的平分线 交边
交边 于
于 ,
,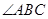 的平分线
的平分线 交
交 ,交
,交 .
.
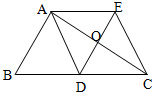
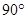 时,求证:四边形ADCE是菱形.
时,求证:四边形ADCE是菱形. 中,
中, ,
, 为垂足.若
为垂足.若 ,则
,则 ( )
( )





 ,连接DE并延长交AB于M,连接BF交CD于N,
,连接DE并延长交AB于M,连接BF交CD于N,
 的值.
的值.