题目内容
如图，平行四边形ABCD中，E为AD的中点，已知△DEF的面积为S，则△DCF的面积为（▲）
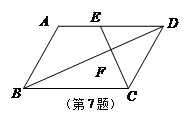
| A．S | B．2S | C．3S | D．4S |
B
∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∴△EDF∽△CBF，∴ED：CB=EF：CF，
∵E为AD的中点，∴ED=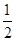
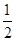AD=BC，∴EF：CF=1：2，
从图中可以看出△EDF与△DCF共一顶点D，所以高相等，∴面积之比为：EF：CF=1：2，
∴当△DEF的面积为S时，则△DCF的面积为2S．故选B．
∵E为AD的中点，∴ED=
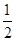AD=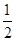BC，∴EF：CF=1：2，从图中可以看出△EDF与△DCF共一顶点D，所以高相等，∴面积之比为：EF：CF=1：2，
∴当△DEF的面积为S时，则△DCF的面积为2S．故选B．
练习册系列答案
相关题目
．分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系．
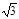）、（4，0）、（3，2
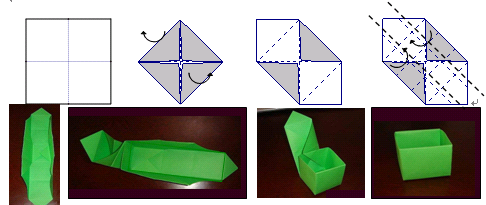
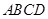的面积为12，
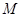是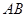
的中点，连接
、
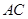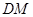，则图中阴影部分的面积是 （ ▲ ）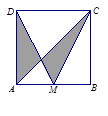
的平分线
交
于
，
，
，则
的长是（ ）
