题目内容
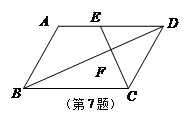
如图,在平面直角坐标系中,A、C、D的坐标分别是(1,2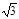 )、(4,0)、(3,2
)、(4,0)、(3,2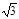 ),点M是AD的中点.
),点M是AD的中点.
小题1:求证:四边形AOCD是等腰梯形;
小题2:动点P、Q分别在线段OC和MC上运动,且保持∠MPQ=60°不变.设PC=x,MQ=y,求y与x的函数关系式;
小题3:在(2)中:试探究当点P从点O首次运动到点E(3,0)时,Q点运动的路径长.
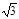 )、(4,0)、(3,2
)、(4,0)、(3,2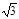 ),点M是AD的中点.
),点M是AD的中点.小题1:求证:四边形AOCD是等腰梯形;
小题2:动点P、Q分别在线段OC和MC上运动,且保持∠MPQ=60°不变.设PC=x,MQ=y,求y与x的函数关系式;
小题3:在(2)中:试探究当点P从点O首次运动到点E(3,0)时,Q点运动的路径长.

小题1:见解析
小题2:

小题3:当P点从O点运动到点E(3,0)时,Q点运动的路径长为
 个单位
个单位(1)∵ yA=yB= ∴ AD//OC,
∴ AD//OC,
又线段AD、OC有共同对称轴直线x=2,
∴OA=CD且AD≠OC
∴ 梯形AOCD是等腰梯形 …………………………… 4分

(2)易证△OMC是等边三角形 所以OM=OC=MC=4
∠MDC=∠QCP=60° 又∠MPQ="60°"
∴∠1+∠2=∠1+∠3=120°
∴∠2=∠3 所以△OMP∽△CPQ
∴
化为 …………………………… 8分
…………………………… 8分
(3)∵0≤x≤4

∴ x=2时,ymin=3 即MQ=3
x=0时, y=4 即MQ=4
x=3时, y= 即MQ=
即MQ=
当0≤x≤2时,Q点运动路径长为4-3=1
当2<x≤3时,Q点运动路径长为
∴当P点从O点运动到点E(3,0)时,
Q点运动的路径长为 个单位
个单位

 ∴ AD//OC,
∴ AD//OC,又线段AD、OC有共同对称轴直线x=2,
∴OA=CD且AD≠OC
∴ 梯形AOCD是等腰梯形 …………………………… 4分

(2)易证△OMC是等边三角形 所以OM=OC=MC=4
∠MDC=∠QCP=60° 又∠MPQ="60°"
∴∠1+∠2=∠1+∠3=120°
∴∠2=∠3 所以△OMP∽△CPQ
∴

化为
 …………………………… 8分
…………………………… 8分(3)∵0≤x≤4

∴ x=2时,ymin=3 即MQ=3
x=0时, y=4 即MQ=4
x=3时, y=
 即MQ=
即MQ=
当0≤x≤2时,Q点运动路径长为4-3=1
当2<x≤3时,Q点运动路径长为

∴当P点从O点运动到点E(3,0)时,
Q点运动的路径长为
 个单位
个单位

练习册系列答案
相关题目
 的图像交点为A,B。
的图像交点为A,B。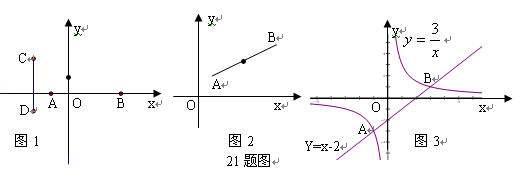
 ABCD的一边BC延长至E,若∠A=110°,则∠1=________.
ABCD的一边BC延长至E,若∠A=110°,则∠1=________. [
[
 ≤
≤ ≤
≤
 ≤
≤
 ≤
≤
 ≤
≤